理化学研究所（理研），東京大学，大阪大学は，機械学習におけるニューラルネットワークの表現能力を応用して，固体系の電子状態に関する第一原理計算を精密に行なう手法を提唱した（ニュースリリース）。
結晶の格子構造や導電性などの性質は，結晶を構成する原子や電子の集団的な振る舞いによって決定される。原子や電子の運動を量子力学に従う第一原理計算を用いて調べることにより，結晶のさまざまな化学的性質や外場との応答を予測することが可能になる。
ただし，膨大な数の粒子を扱う理論やシミュレーション手法は極めて困難な「量子多体問題」の一つであり，いまだに確立されていない。この超難問に対して近年，機械学習におけるニューラルネットワークが有効なのではないかという見方が強まっている。
研究グループは，固体結晶の性質の中でも特に重要な「基底状態」と「バンド構造」を調べる計算アルゴリズムの開発に焦点を絞った。
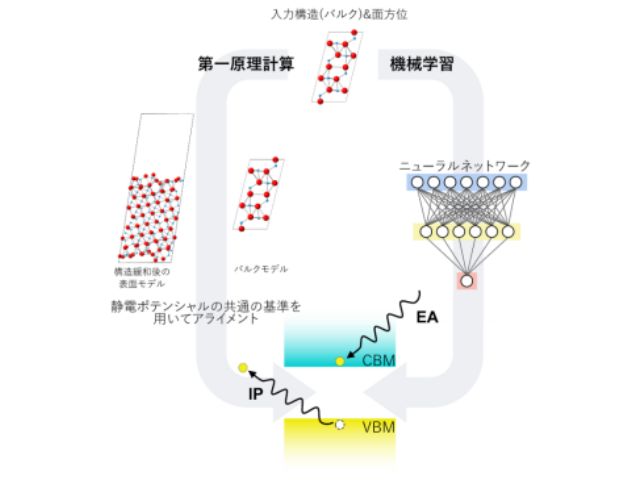
第一原理計算において，あらゆる電子構造から最も安定な状態を探すには，膨大な計算量が必要。そこで，電子状態を与える多体波動関数を，ニューラルネットワークによって近似する新手法を提案した。これにより，広範な物質において，計算量を大幅に削減しつつ，厳密な計算手法に対して「化学精度」と呼ばれる近似精度を達成した。
これは，この手法による計算が，化学反応を予測できるほど精密であることを意味するという。さらに，従来の近似手法では取り扱いの難しい電子相関の強い領域においても，この手法が有効であることを示した。
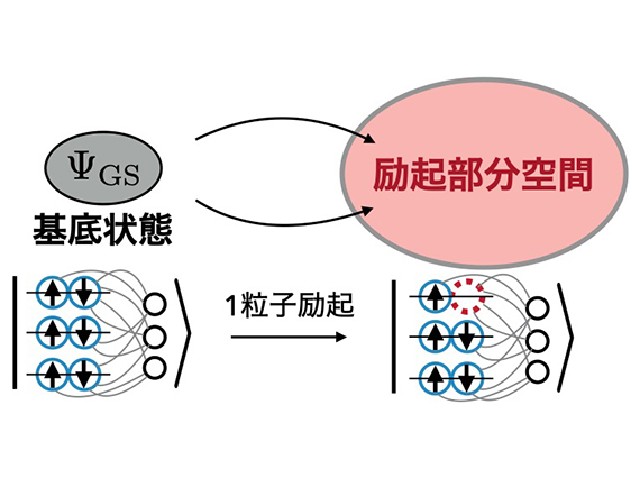
バンド構造は，固体結晶の電子が持つエネルギーと運動量の関係を表す。レーザー照射への応答や熱・電気的な伝導性などの特性を最も端的に表すため，重要な概念となる。しかし，多体波動関数によるバンド構造は基底状態のような最適化を通して計算できないため，その計算にはより大きな困難を伴う。
一方で，固体結晶中の励起が電子やプラスの電荷を持つ正孔による1粒子近似によって本質的に規定されることに着目すると，探索すべき空間を大幅に制限できる。実際に，基底状態を記述するニューラルネットワークから得られる励起部分空間（粒子がとりうる状態が制限された空間）を活用すれば，ポリマー系のバンド構造を計算できることを示したという。
強い電子相関を第一原理計算で記述する波動関数理論を構築することは，現代物質科学の根底にある最も大きな課題の一つ。この成果は，複雑な電子構造の効率的表現を探究する上で，新たな方向性を開拓したといえ，ニューラルネットワークを用いて量子多体問題に挑むという潮流にさらなる発展を促すものだとしている。
