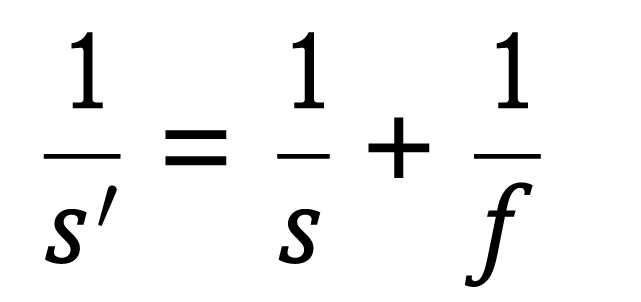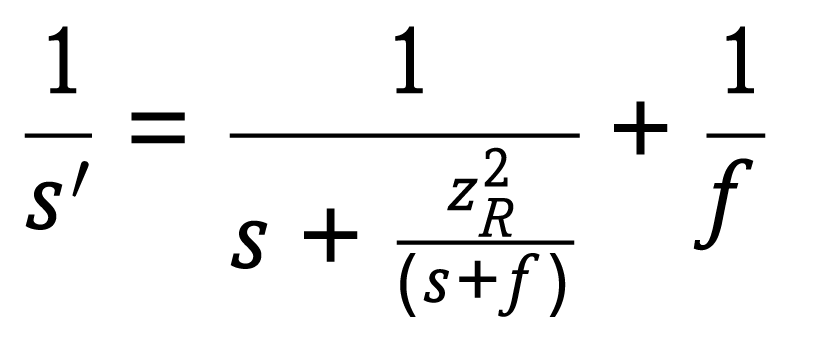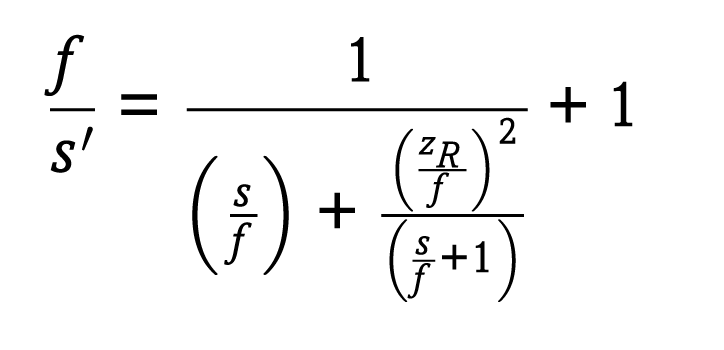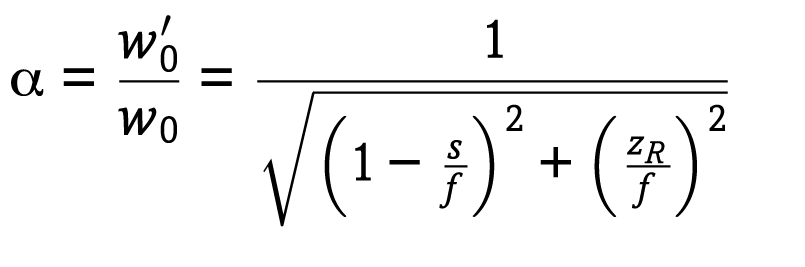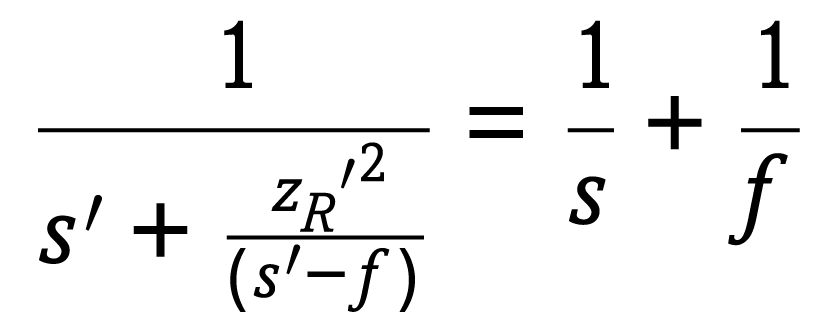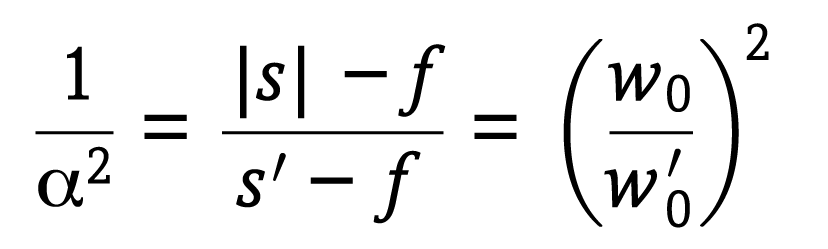1 はじめに
レーザーオプティクスアプリケーションの多くで，レーザービームは理想的なガウス分布に沿った放射強度プロファイルを持つガウシアンと想定されている。本稿では，実際の光学システムで必要になるガウシアンビームの操作について，関係する方程式を示しながら解説する。

2 ガウシアンビームの操作
レーザー光学システムの多くでは，「元々の」ビームを単純に用いるのではなく，レーザービームの操作が要求される。この操作は，レンズ，ミラー，プリズム等の光学部品を用いて行なわれる場合がある。以下に，最も一般的なガウシアンビーム操作をいくつか紹介する。

3 ガウシアンビームに対する薄レンズの公式
理想的な薄レンズによる結像は，以下の公式を用いることができる^1）：

（2-1）

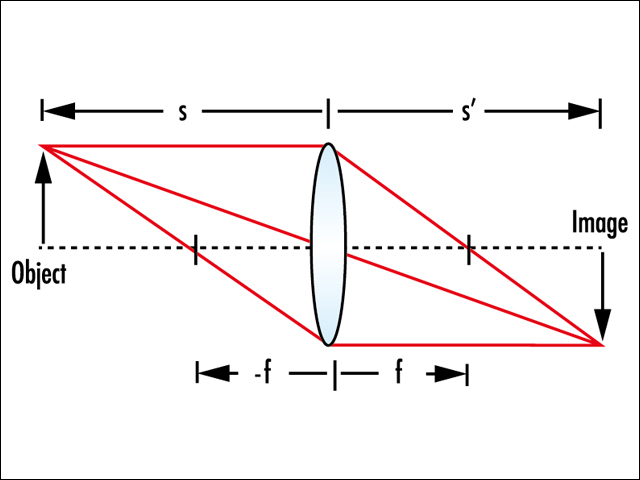
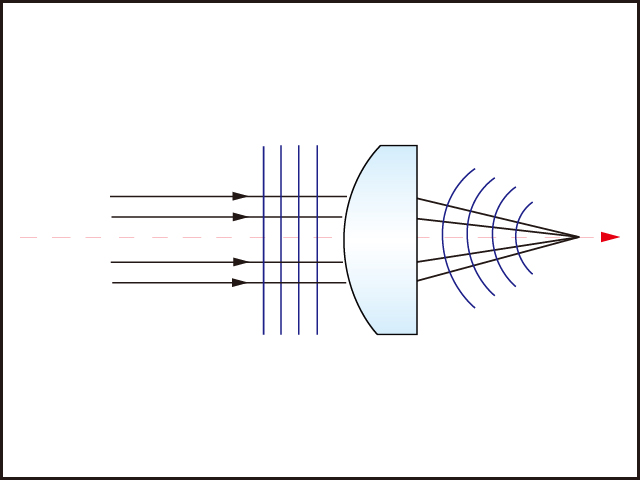
式（2-1）において，s′はレンズから像までの距離，sはレンズから物体までの距離，fはレンズの焦点距離になる。物体と像がレンズに対して各々反対の位置にある時，sは負の値でs′は正の値をとる。この公式は，実物のレンズの厚さを無視しているため，現実世界の単なる近似になる（図1）。

結像のアプリケーションでの適用に加え，この薄レンズの公式は，入力ビームのウエストを物体として，また出力ビームのウエストを像として扱うことで，ガウシアンビームの集光にも適用できる。ガウシアンビームは，収差のない理想的なレンズを通過した後でもガウシアン分布を維持する。1983年，Sidney Selfは，ガウス伝播を考慮に入れた薄レンズの新たな公式を作った^1）：

（2-2）

レーザーから一点集光するまでの全距離は，sの絶対値をs′に加算することで計算できる。式（2-2）の両辺にfを乗算することで無次元の形式にも書き表すことができる：

（2-3）

この公式は，z_R/fが0に近づくにつれて標準の薄レンズの公式に近づくため，長い焦点距離を持つレンズに対してその薄レンズの公式が使用できるようになる。式（2-2）と（2-3）は，レンズを通して像を結んだ後のビームウエストの位置の特定に用いることができる（図2）。

像距離（s′/f）と物距離（s/f）の関係をレイリー領域（z_R/f）別に正規化したプロットは，物距離によって可能な出力側ウエストの位置を教えてくれる（図3）。このプロットは，レンズを通じて一点に集光するガウシアンビームを従来の薄レンズの結像公式と比べた場合に，いくつかの大きな違いがあることを示す。

ガウシアンビームの結像は，生じ得る最小と最大の像距離の両方を持つのに対し，従来の薄レンズの結像公式はそれを持たないこと。再集光するガウシアンビームの像距離は，–fの場所ではなく，–（f+z_R）で最大になること。

そしてプロット上のs/f=–1およびs′/f=1の地点，即ち入力側ウエストが正レンズのフロントフォーカスポイントにある時，レンズのバックフォーカスポイントが出力側ウエストになることである。

ビームがレンズを通過した後のビームウエストとレイリー領域を理解するには，次式で与えられるシステムの倍率（α）を知っておく必要がある：

（2-4）

ここで，w₀はレンズ通過前のビームウエスト，w′₀はレンズ通過後のビームウエストである。ガウシアンビームの薄レンズの公式は，レンズ通過後のビームのレイリー領域（z′_R）を含めた形で次のように書き換えることができる：

（2-5）

上記公式は，レンズがビームウエストにある場合（s=0）は，分解される。倍率の自乗の逆数は，ビームウエストサイズと位置を関連付けるために用いることができる^2）：

（2-6）

参考文献
1） Self, Sidney A. “Focusing of Spherical Gaussian Beams.” Applied Optics, vol. 22, no. 5, Jan. 1983.
2） O’Shea, Donald C. Elements of Modern Optical Design. Wiley, 1985.

■Gaussian Beam Propagation 2
■Edmund Optics Japan Co., Ltd.

＜お問合せ先＞
エドモンド・オプティクス・ジャパン㈱
TEL: 03-3944-6210
E-mail: tech@edmundoptics.jp
URL: www.edmundoptics.jp