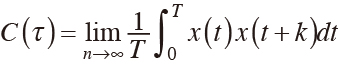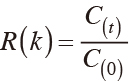4.　曳航水槽実験による模型船底の壁面摩擦計測

本章では実験は曳航水槽実験の結果^7〜9）を紹介する。広島大学曳航水槽実験装置を使用した。曳航水槽の実験区間は長さ80 m，幅8 m，深さ3.5 mである。本実験は北海道大学（村井祐一）との共同プロジェクトで実施された。この曳航水槽実験装置に模型船（図9）を固定し，曳航実験を行った。気泡を入れる前（単相流）の実験は船速0.25 m/sから3.00 m/sまで0.25 m/s刻みで上昇させ測定を行った。

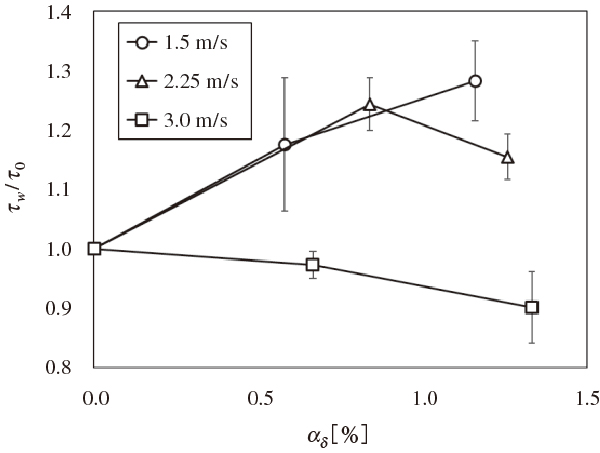
流速が1.50 m/s，2.25 m/s，3.00 m/sにおいて気泡の注入を行った。各流速におけるボイド率の変化によるせん断応力の増減を図10に示す。縦軸に単相流におけるせん断応力の平均値との比であり気泡注入によるせん断応力の増減を示し，横軸に境界層内ボイド率を示す。流速1.50 m/sではボイド率の上昇に伴ってせん断応力が増加し，流速2.25 m/sではボイド率0.84％において極大値を取り，流速3.00 m/sではボイド率の上昇に伴いせん断応力が低減していることが確認できる。単相流においても標準偏差があることに注意する必要があるが，結果よりボイド率と流速が高いほど抵抗低減効果を得やすいという従来研究^10）と同様の傾向をレーザーせん断応力計でも確認した。

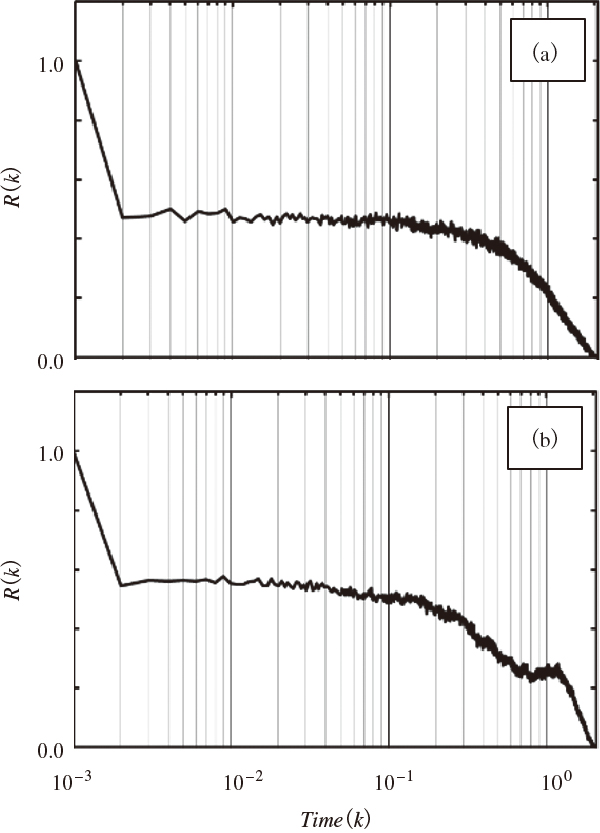
次に，摩擦抵抗低減効果が起きていると考えられる流速3.00 m/sのボイド率1.4％における単相流におけるせん断応力の時間変動は気泡が注入されたときの変化に注目した。注入された気泡群がクラスタ化してボイド波を形成し，下流に流れていくに伴って周期性を持つことが示されている^5）。この周期性を持ったボイド波がせん断応力に対して影響を及ぼし，せん断応力もまた気泡を注入した際に周期的な変動を持つと予想している。そこで，せん断応力の周期性を調査するためにせん断応力の時間変動の自己相関係数の算出を行った。単相流および気泡流における解析結果を図11に示す。ここで，自己相関関数を定義する。ただし，定義上はアンサンブル平均を用いるが，曳航水槽実験はアンサンブル平均を得る回数を確保するのが困難なため，データサンプリングの制限が生じやすい。ここでは時間平均を用いて自己相関関数を定義すると式⑹のようになる。

⑹

tは時刻，1周期分の時間Tとし，タイムラグをここではτとした。自己相関関数はラグkを用いて式⑺より算出した自己相関係数であり，横軸はタイムラグを示す。

⑺

図11に自己相関関数の解析結果を示す。結果より0.002秒において相関係数が急激に降下している。これは乱流において，応力の類似性が低く同周期の波形が少ないことが考えられる。これは乱流において自然な結果である。ここでボイド率1.33％において送った時間が1秒直後から急激な自己相関係数の上昇が確認できる。これは周期に換算すると1 Hz程度のせん断応力変動であり，気泡が影響していることが考えられる。今回の実験では可視化によって連続注入された気泡が遷移して，周期性を伴って下流へと流れていく様子が確認されている^11）。