東京大学と加ブリティッシュコロンビア大学は，伝導体の自由エネルギーにリフシッツ不変量と呼ばれる対称操作で変化しない不変量が存在すると超伝導秩序が光に線形で応答することを見出し，それが現れるかどうかを判別する分類理論を構築した（ニュースリリース）。

超伝導秩序を光で制御したり増幅したりする試みがされている。超伝導秩序が強まると，より高い温度や強磁場の環境下でも超伝導状態を保てるが，これまで超伝導秩序と光の結合が弱く，一般的に超伝導秩序は光と非線形な応答しか示さないと考えられていた。

ところが最近，マルチバンド超伝導体に注目すると超伝導秩序が光に対して線形に応答するケースが見つかってきている。しかし，一般に超伝導秩序が光に対して線形に応答する条件や，また特に二次元や三次元の物質で現れる条件はわかっていなかった。

研究グループは，マルチバンド超伝導体のレゲットモード（異なる秩序変数の位相の差が振動する集団励起モード）が光に対して線形に応答するのは，熱力学な性質を記述する自由エネルギーにリフシッツ不変量と呼ばれる対称操作によって変わらない不変量が存在するときと見出した。

リフシッツ不変量は秩序変数について一階の空間微分を含む形をしており，物質が空間反転対称性を破るときにしか存在できないと考えられていたが，空間反転対称性の破れは必ずしも必要ではなかった。

超伝導体においてリフシッツ不変量が存在できるのはどのようなときかを，数学の一分野である群論を利用して全ての結晶構造とクーパー対の対称性について調べた。

群論は対称性を記述する数学の理論であり，着目する物質を不変に保つような対称操作に対してリフシッツ不変量が自明な表現を持つかどうかを確かめることによって，自由エネルギーにリフシッツ不変量が出現するかを判定できる。

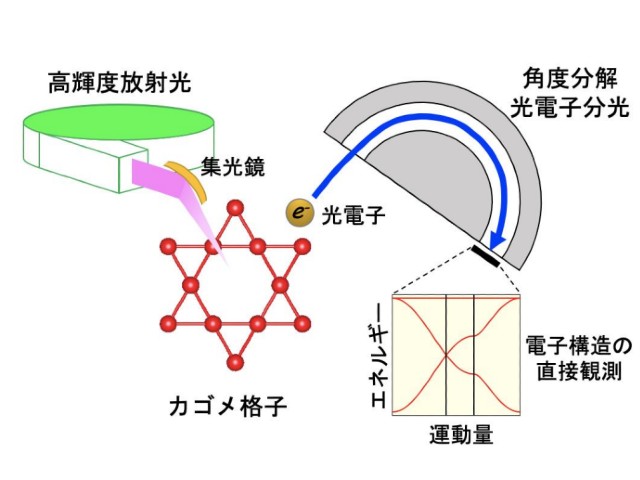
この結果をカゴメ格子超伝導体に適用したところ，通常のカゴメ格子ではリフシッツ不変量が存在しない一方，電子の飛び移りやすいボンドと飛び移りにくいボンドがあるようなカゴメ格子ではリフシッツ不変量が存在することがわかった。

実際に微視的な理論に基づいて線形応答領域の光学伝導度の計算を行なうことで，後者の場合は超伝導ギャップ以下の周波数のところにレゲットモードに由来する共鳴ピークを確認できた。

これ以外のパターンの不均一なボンドを持つカゴメ格子超伝導体についても分類理論を適用することで，光に線形で応答するレゲットモードが存在できるかどうかを調べることができる。

研究グループは，レーザー光を用いて超伝導秩序を高速に制御したり，光によってマルチバンド超伝導体の微視的性質を解明することへつながる成果だとしている。