筑波大学の研究グループは，非線形システムをよりよく表現できる疑似線形化法を提案した（ニュースリリース）。

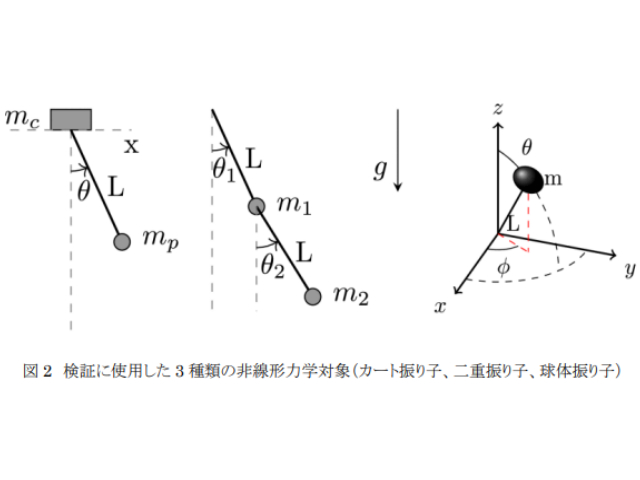
自然現象に基づくほとんどの工学システムは物事の関係が比例関係ではない非線形となっている。非線形システムの安定性を解析し，これを制御する仕組みを設計することは，システム制御理論において重要な問題となる。

非線形システムの安定性を調べるには，リアプノフの線形化（間接法）が最も一般的で有用なアプローチの一つで，これにより，線形近似に基づいて平衡点周辺の局所安定性を調べ，よく知られている線形制御理論を適用することができる。

しかしながら，単一の平衡点の安定性を調べるためには便利であるものの，平衡点が無数にあるシステムの場合，すべての平衡点を個別に調べるのは現実的ではない。

研究では，相空間における平衡点の拡張として平衡空間という新しい概念を，ベクトルと行列を用いた数式により提案した。平行空間は無数の連続的に存在する平衡点からなる空間と定義され，システムの状態変数が平行空間にある場合，時間が変化してもシステムの状態は変化しない。

この概念は，これまでの平衡多様体の考え方と同等だが，平衡空間の次数がゼロの時には単一の平衡点を表すこともできることから，より幅広いシステムに適用できると考えられるという。

また，この平衡空間の概念に基づいて，リアプノフの線形化法を拡張した疑似線形化法を提案した。これにより，線形の形式で表される非線形システムを導出することができ，既知の線形制御理論を適用して，安定性の解析や制御の設計が可能になる。

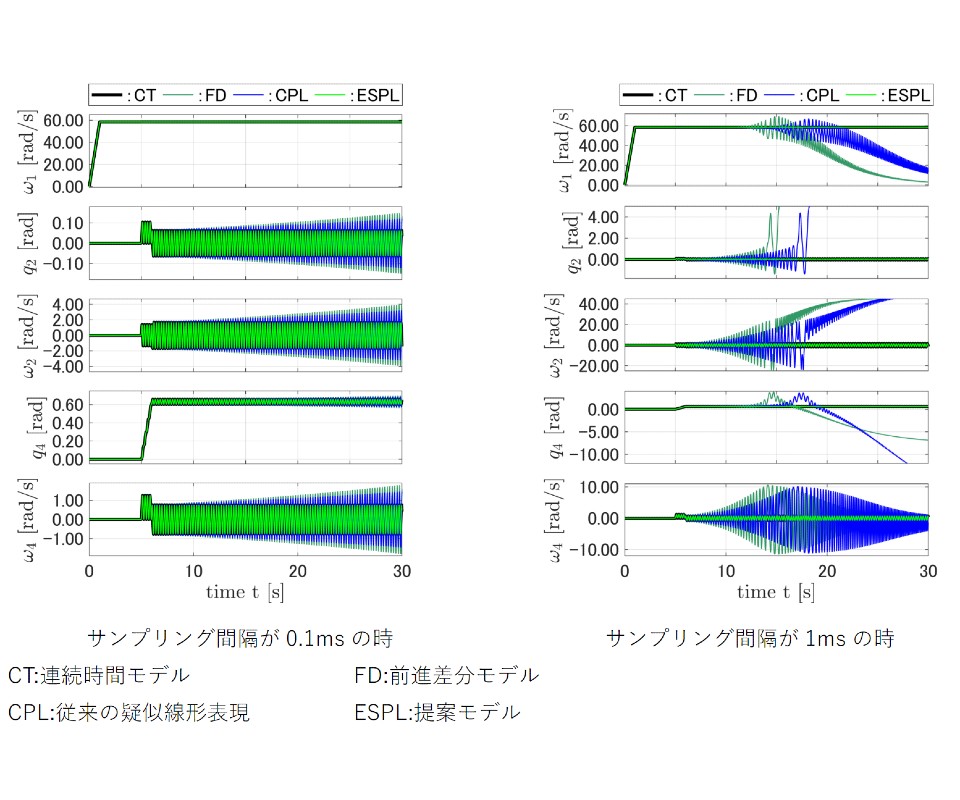
実際に，この疑似線形化を用いて，人工衛星や宇宙船の姿勢制御アクチュエータとしてよく使用されるCMG（Control Moment Gyro）システムの非線形連続時間モデルから離散時間モデルを導出した。

その結果，この離散時間モデルが，よく知られた前方差分や平衡点法に関する線形化や従来の疑似線形表現によって導出された離散時間モデルに比べて，連続時間モデルの応答に近い応答を生成することが分かった。また，離散時間のサンプリング間隔（計算機での離散時間の間隔）を大きくしても，提案したモデルの精度が保たれることも示された。

今回提案した平衡空間の概念および疑似線形化の手法に関しては，安定性の解析や制御設計への適用をさらに検討する必要があるという。また，大きなサンプリング間隔に対しても高精度の離散時間モデルが導出できることから，研究グループは，低スペックの計算機，低計算コスト，低価格での制御システムの実装が可能になるとしている。