2.　幾何光学

2.1　Fermatの原理

本章では結像について取り扱う。光の結像は光が起こす最も有用な現象の一つである。光の伝播を表わす方法は色々あるが，光線を使う表記が直感的で分かり易い。空間内の点Aから点Bの間が停留値となるFermatの原理で表される。

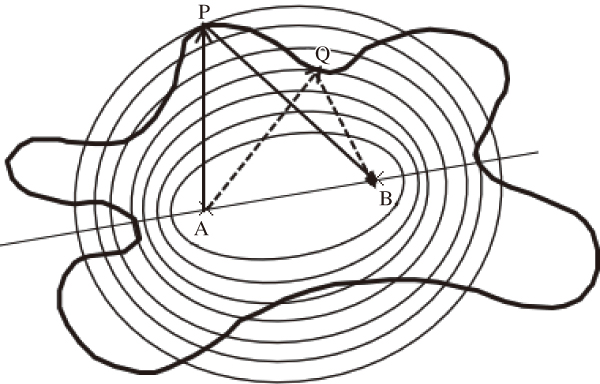
例えば図1のような閉曲面内に点AとBを考える。ここでAを出て閉曲面で反射してBにいたる光線を求めてみる。簡単のためここでは2次元で考える。

反射点はAとBを焦点とする楕円群を考え，楕円と閉曲面の接点として求めることができる。接し方には楕円を外側から小さくして行った後に交差状態に入る場合と，逆に内側から大きくして行った後に交差状態に入る場合の2種類がある。前者はPに対応する光路が極大の場合，後者はQが相当し極小の場合に相当する。楕円の大きさを変えて，全ての接点を求めればAから反射してBに行きつく箇所が分かる。

光の伝播を光線として取り扱うのが幾何光学である。波長は実質的に0と考える。これに対し光を波として扱い，干渉を考えるのは波動光学と呼ばれる。幾何光学は昔から研究され，学問的には枯れた分野と見なされて教育の場で詳しく教えられていない。しかし，光学装置のレンズやミラーの曲率，厚さ，材料の具体的な値を決めるのは幾何光学で，その有用性は計り知れない。幾何光学の本質をつかむことは光工学では最重要事項の一つである。

現代の光学設計は幾何光学と計算機を組み合わせたシステムになっている。光学設計は自動設計システムの最も早い成功例である。最も精緻と言われる半導体リソグラフィ用の投影光学系の設計もこれで行われている。