1. はじめに

液晶ディスプレイ(以下,LCD)の普及に伴い,液晶という言葉が身近なものとなった。液晶は,三次元的な配向秩序により異方性を有する結晶と,配向秩序がなく流動的な等方性液体の間に発現する中間相である。異方性と流動性の両性質を兼ね備えるため,電磁場や擦り,延伸などの外力により分子配向の制御が可能となる。LCDの中では液晶分子が偏光のシャッターとして利用されている。
高い複屈折性を有する液晶分子は,円偏光反射フィルム2),レーザー発振用フィルム3),焦点可変液晶レンズ4)およびホログラム材料5)など様々な光学材料への応用が期待される。従来,光学的異方性を有する材料は,有機および無機化合物の単結晶の合成,精密加工や積層および蒸着といった高度な技術に大きく依存してきたが,液晶の優れる点としては自発的な分子配向の制御が可能であることから,加工性の付与や低コスト化に寄与できるため,高複屈折性液晶分子の開発には意義がある6)。
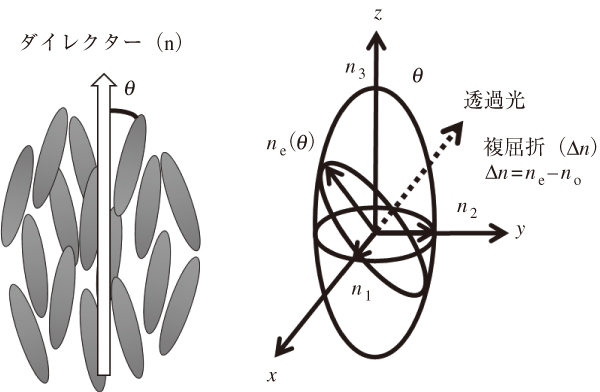
複屈折(Δn)とは,ある方向間における屈折率の差である。正の一軸性の複屈折性を有する棒状分子のN相においては一般に,分子長軸方向の異常光屈折率(ne)および常光屈折率(no)の差(Δn=ne–no)を意味し,図1に示す屈折率楕円体で表される6)。
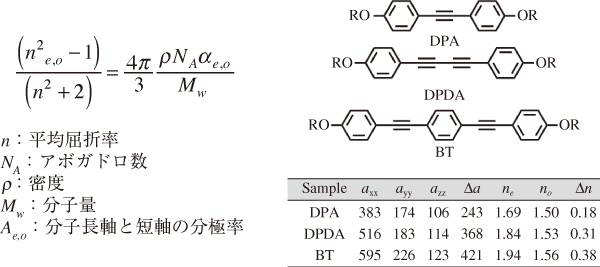
屈折率はLorentz-Lorenz式で表されるが,異方性媒体である液晶では図2に示すVuksの式によりneおよびnoにそれぞれ拡張される7)。そのため,複屈折の大きな分子(材料)を作りたい場合は,特に高いneを発現する分子の合成が有効であり,大きな分子長軸方向の分極率(αx)を有する分子を設計する必要がある。その方法として,分子構造的観点からは,芳香環や不飽和結合の直線的な連結によるπ共役系構造,シアノ(CN)基,イソチオシアネート(NCS)基などの分極率の大きな置換基の導入,炭素数の短い置換基が有効である。図2に密度汎関数法(DFT)を用いた分子計算により求めた,分子分極率の成分と,実際に測定した屈折率および複屈折の値を示す。π共役系の拡張は,主にαxの向上に寄与し,これら分極率特性は,実測の屈折率特性とも大まかに一致していることがわかる8)。