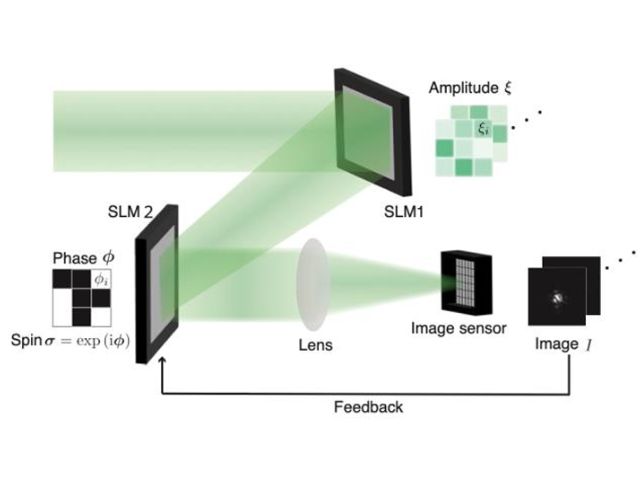
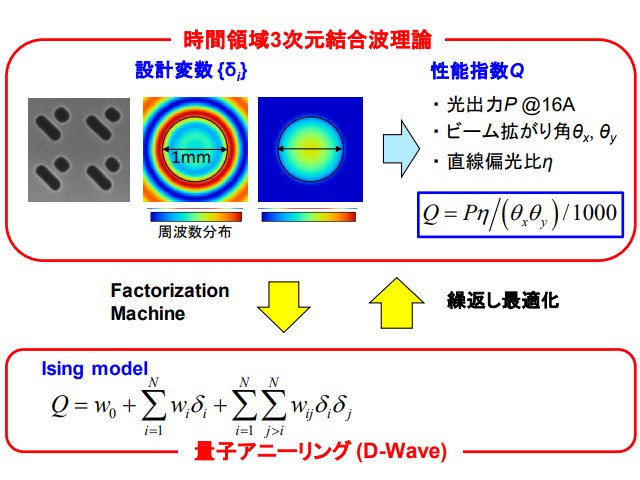
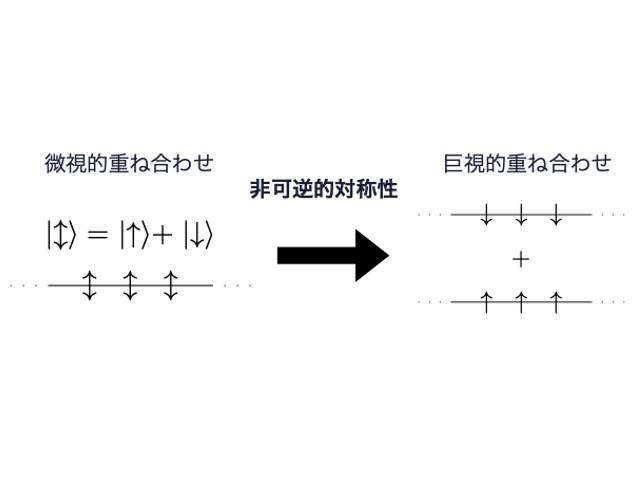
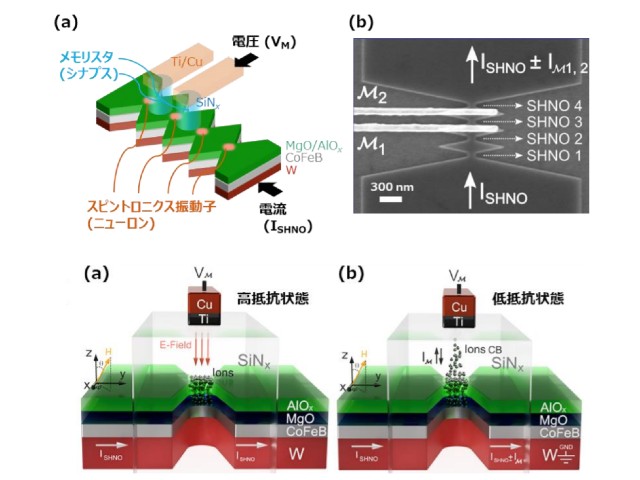
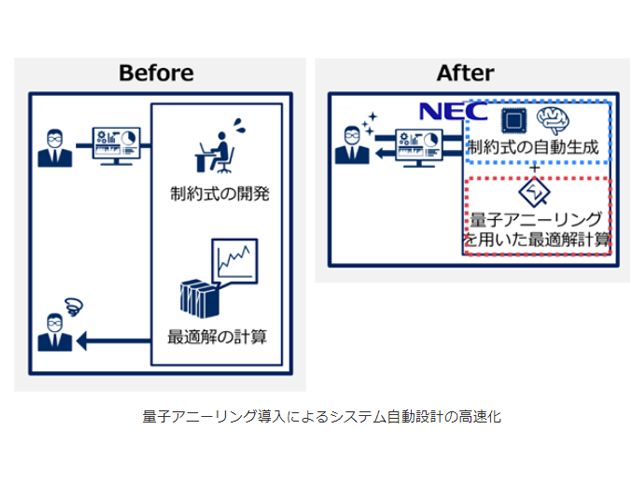
早稲田大学の研究グループは，量子アニーリングマシン（イジングマシン）のハードウエア上の制約による，入力可能な問題規模の制限を解消するため，最適性を失わずに大規模な問題を小さな問題に分割する条件を解明した（ニュースリリース）。
組合せ最適化問題の最適解を得るために注目されているイジングマシンにはまだ課題が多い。特に，ハードウエア上の制約から入力可能な問題規模制限されており，現状のイジングマシンで大規模な問題を直接解法することは難しかった。
既存研究では，発見的な手法によって，大規模な問題を小さな問題に分割してイジングマシンで解法していたが，分割された問題の答えが，元の大規模な問題の答えと一致しているか理論的な条件は未解明のままだった。
今回の研究では，イジングマシンに入力可能な問題規模の制限を解決するために，まず，最適性を失わずに大規模な組合せ最適化問題を小さな問題に分割する条件を解明した。これにより，イジングマシンによって，条件を満足した小さな問題を解法すれば，元の大規模な問題の答えと一致することを証明した。
また，大規模な問題からうまくこのような条件を抽出し，元の大規模な問題をイジングマシンで解法可能な問題規模まで小さくして，繰り返し解法する新たなアルゴリズムを提案した。このアルゴリズムは，理論的な裏付けのもとに大規模な問題を小さな問題に分割して解法するため，従来技術に比較して精度よく元の大規模な問題を解法することができる。
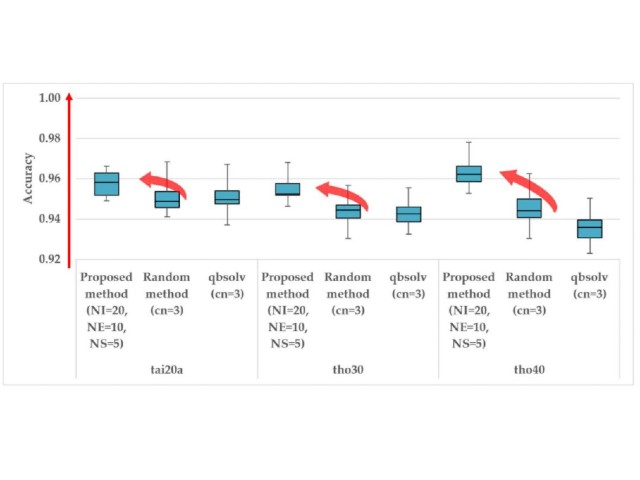
実際に，実イジングマシンで解法することができる問題規模に対して，8倍～32倍の大きな問題について，提案手法と従来手法（ランダム手法とqbsolv手法）とを比較した結果，今回の手法で得られる答えの精度が高いことが分かった。
従来イジングマシンではハードウエア制約によって利用可能なビット数が制限されていたために規模の大きな問題は解くことが困難だったが，この手法を使うことによってイジングマシンで計算することができる。
そのため，量子アニーリングマシンを含むイジングマシンを使った，現実世界の組合せ最適化問題への活用事例を広げることができると考えられるという。また，この研究は古典計算機とイジングマシンとを併用して問題を解法する取り組みでもあり，イジングマシンの活用範囲が大幅に広がるとする。
研究グループは今後，さらに実世界に見られるさまざまな問題にこの手法を適用し，有効性を検証していく必要があるとしている。
