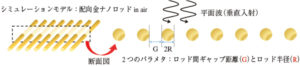
2.　シミュレーション

半径がRで無限長さを持つ金ナノロッドが，ギャップ距離Gの間隔で周期的に並んだ2次元モデルを作成し，平面波が垂直入射した時の反射・透過・吸収をシミュレートした（図2）。金の屈折率はPalikによる値^12）を用い，シリカの屈折率は1.44とした。結果を図3にまとめる。光吸収スペクトルにおいて，電場成分が金ナノロッドの長軸に直交するp偏光に対してのみ，局在SPPに帰属されるピークが現れた。

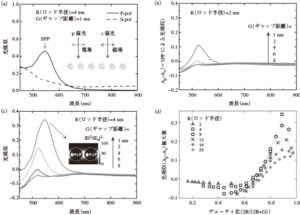
これに対し，s偏光に対して見られる短波長側の吸収は金の内部遷移に起因する。得られた光吸収スペクトルに対し，p偏光での吸収からs偏光での吸収を差し引くことで金の内部遷移の寄与を排除し，SPP励起による吸収を見積もった。図3（b）にロッド半径R=2 nmでギャップ距離G=1〜8 nm，（c）にR=4 nm，G=1〜8 nmの構造に対する結果を示す。R=2，4 nm両者ともG=1 nmで最も強くSPPが励起されることがわかる。

また特にR=4 nm，G=1 nmの際にSPP励起に伴う光吸収が大きくなり，吸収ピーク波長の光を入射したときの光エネルギーの分布を見ると，ロッド間を中心に増強電場が発生していることがわかった（図3（c）挿入図）。R=2〜20 nm，G=1〜20 nmの間でモデルを系統的に変化させ，SPPに起因する光吸収の極大値を構造周期に対する直径の比（2R/（2R+G））で整理したところ，どのRに対しても比が0.9付近で吸収が極大となることがわかった（図3（d））。

また，特にR=4および8 nmで極大値が大きくなった。これらの結果から，SPPを強く励起できる構造として，ロッド半径R=4〜8 nm，構造周期2R+G=9〜18 nm程度の構造が望ましいことがわかる。後述するように，実験に使用した配向性メソポーラスシリカ薄膜の周期は10 nmであり，この薄膜にギャップ距離を制御して金ナノロッドを並べることができれば，SPP励起に最適なメソグレーティング構造となることが期待される。

3.　実験結果と考察

一軸配向したメソポーラスシリカは既報^13）に基づき作製した。P123，Brij56の2種類のブロックコポリマーを，塩酸とイソプロパノールの混合溶液に溶解した後，そこにテトラエトキシシランを加え2時間撹拌した。シリカガラスにポリイミドを塗布後，ラビング処理し，この基板を上記の均一溶液に浸漬して，ディップコーティング法によりメソポーラスシリカ薄膜を作製した。これを400℃で30分アニールしポリマーを除去した後，ウェットエッチングにより表面にメソ周期構造を露出させ^11），電子線蒸着装置を用いた斜め蒸着により金メソグレーティング構造を作製した。

基板を70°傾けて金を堆積したサンプルのSEM画像（top-view）を図4（a）に示す。画像中明るい部分が金であり，金がメソポーラスシリカの配向方向に沿って，y方向にロッド状に成長していることがわかる。しかしながら，メソポーラスシリカ基板の周期構造を完全に反映しているわけではなく，ところどころ隣接するロッド同士がつながったり，長軸方向に伸びるロッドが途中で切れたりしている。SEM像の2次元フーリエ解析によりx軸方向の構造周期を見積もると約20 nmであり，メソポーラスシリカ薄膜の周期10 nmの倍である。

これは斜め蒸着の際，基板に到達した金原子がメソシリンダーの凹凸を乗り越えて基板上を拡散するためである。したがって，拡散を抑えればメソポーラスシリカの周期に近い構造が得られる。例えば，金より融点が高く，拡散の起こりにくい白金を同じ条件で堆積させると，10 nm程度の周期構造が得られる（図4（b））。

得られた金メソグレーティング構造に対して透過率測定を行った。測定の模式図を図5（a）に示す。ハロゲンランプを光源とし，図4のy軸を回転軸として入射角を0°から60°まで変化させながらp偏光とs偏光について測定を行い，透過率の角度依存性，偏光依存性，波長依存性を調べた。p偏光（図5（b））にのみ見られる波長650 nmの透過率の減少はSPPの励起による。シミュレーションと同様，p偏光のみでSPPが励起されることがわかる。SEMで見られる通り，得られた構造は無限の長さを持つまっすぐなロッドではないが，マクロスコピックな光学応答はシミュレーションで用いた理想的なメソグレーティング構造で解釈可能であり，半定量的にシミュレーションで再現可能であった^14）。