東北大学，京都大学の研究グループは，ゆらぐ機械が本質的にできないことを表現する新しい不等式を見出した（ニュースリリース）。
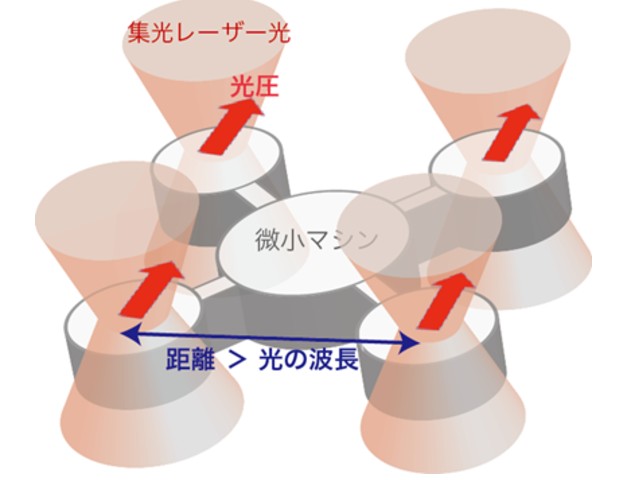
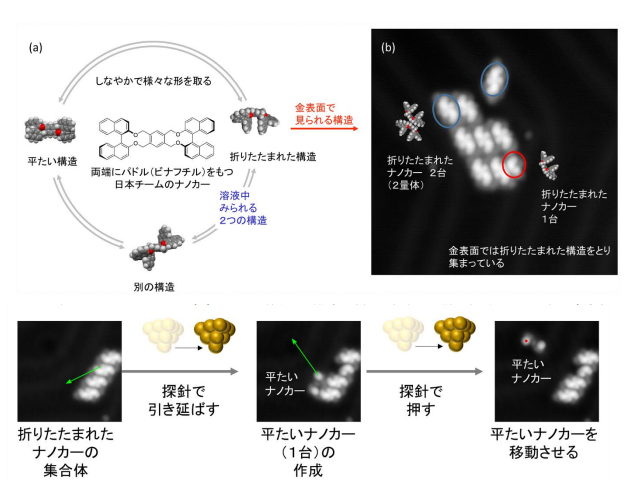
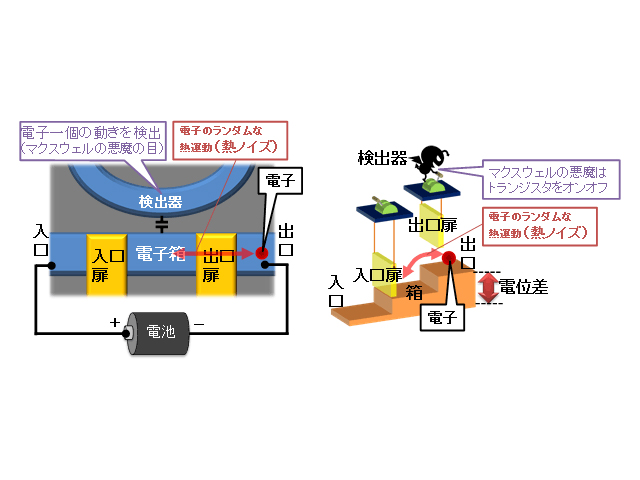
近年，生体内で働く大きさ10nmくらいの小さな機械に関する物理法則が議論されてきた。特に，小さな機械では周りの分子の影響を受けて相対的に大きくゆらぎながら作動するので，ゆらぐ機械の本質的限界を明らかにすることが問題になっていた。
研究では，ゆらぎを伴う機械の性能について，その基本限界を定式化した。鍵となるのが，ゆらぎと応答の関係。一般に，ゆらぎの大きさと応答の大きさには相関がある。例えば，水に大きさ100nm程度の小さな粒子が浮かぶとき，粒子は水分子との衝突により右往左往する。
ゆらぎの大きさは単位時間あたりの平均2乗変位（拡散係数）によって特徴づけられる。この粒子に力を加えて応答をみると，小さな粒子は平均的にはある速さで動くので，力の大きさに対する速度の大きさ（易動度）がその応答を特長づける。
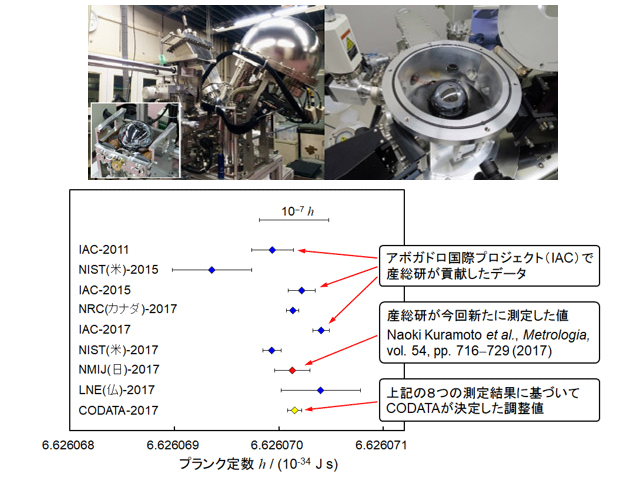
この例では，ゆらぎが応答に比例し，その比例係数に絶対温度，気体定数，アボガドロ定数があらわれる。これは「アインシュタインの関係式」とよばれ，ゆらぎと応答の普遍的な関係の最初の例になっている。
ただし，この普遍的な関係は，応答を与える前は「巨視的な流れ」がない状態（平衡状態）にあることを前提にしている。しかし，問題にしているゆらぐ機械については，エネルギーの注入と出力がバランスしている非平衡定常状態で作動しているので，アインシュタインの関係式は成立しない。
そこで，その破れ方からエネルギー散逸を評価することを可能にする有用な公式が見出されたりするなど，ゆらぎと応答の関係からシステムの特長を捉える試みがなされてきた。研究では，応答の基本的限界を表現する不等式をゆらぎに着目して導いた。
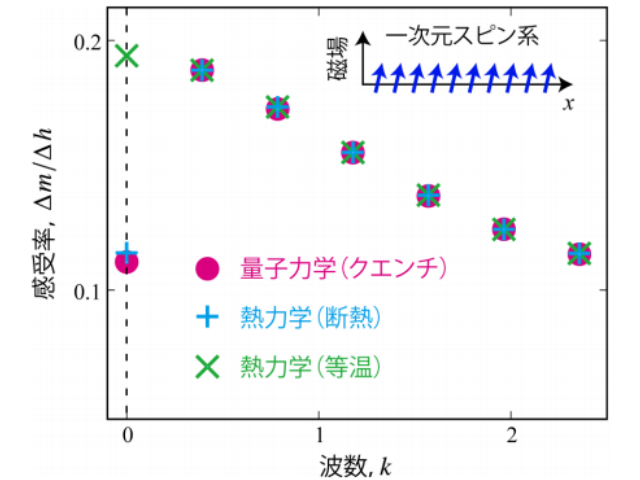
理論的には，系の条件をわずかに変えたときの確率分布の変化を「相対エントロピー」とよばれる情報論的な量によって定量化することを出発点にとる。この量は二つの意味で重要になる。第1に，その操作に対する測定量の変化（応答）とゆらぎを相対エントロピーによって不等式で結びつけることができる。第2に，「物理的な問題」においては，その相対エントロピーが熱力学エントロピーの変化と関係づけられる。
この二つを組み合わせると，ゆらぎ，応答，エントロピー変化が不等式で関係づけられる。特に，変化させる条件と測定量に応じて様々な形の不等式を導くことができる。近年見出されてきた関係式を含むだけでなく，新しい不等式を見つけるための基本的な道具になっている。
今後，新しい不等式を使って，個々のゆらぐ機械の性能を特長づけることにより，生体内分子機械の設計原理が不等式によって解き明かされることが期待されるとしている。
