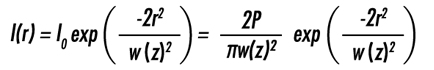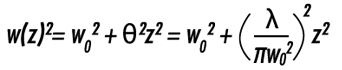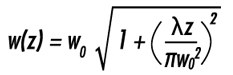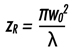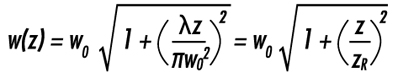1 はじめに
レーザーオプティクスアプリケーションの多くで,レーザービームは理想的なガウス分布に沿った放射強度プロファイルを持つガウシアンと想定されている。本稿では,ガウシアンビームの定義に必要な項目について,関係する方程式を示しながら解説する。
2 ガウシアンビームの定義
実際の全てのレーザービームは,この理想的なガウス的性質からある程度はずれている。ビーム品質係数としても知られているM2値は,現実のレーザービームの性能を回折限界のガウシアンビームのそれと比較する1)。
ガウシアン強度分布は,ビームの中心を軸に左右対称であり,ビームの中心から半径方向の距離が大きくなるにつれ,その強度が小さくなる(図1)。この分布は,式(1-1)で表される2)。

式(1-1)において,I0はビーム中心でのピーク放射強度,rは軸からのラジアル方向距離,w(z)は放射強度が I0の1/e2(13.5%)になる地点のレーザービームの半径,zは波面がフラットになる面からの伝播距離,Pはビームの全パワーになる。
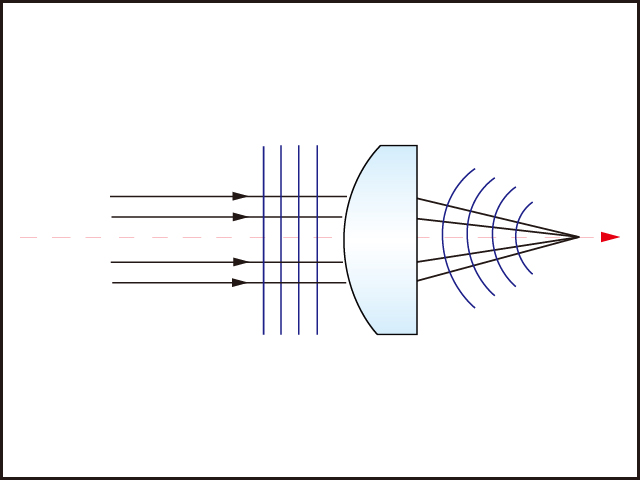
しかしながら,この放射強度分布は,ビームが空間を伝播する時に一定のままではなく,zの関数を含むw(z)に依存する。ガウシアンビームは,回折によってビーム直径が最小値をとるビームウエスト(w0)と呼ばれるエリアの前後で収束し,発散する。
ビームウエストの両側で発散角θの大きさで均等に収束/発散する(図2)。ビームウエストと発散角の大きさはどちらも軸から測定され,その関係は式(1-2)と式(1-3)で表される2)。
上記公式において, λはレーザーの波長, θはファーフィールド近似した発散角である。したがって,θはビームウエスト近傍でのビームの発散を正確には表さないが,ビームウエストからの距離が増すにしたがい,より正確になる。式(1-3)から分かるように,ビームウエストが小さいと発散角は大きくなり,ビームウエストが大きいと発散角は小さく(よりコリメートビームに)なる。
これは,ビームエキスパンダーを用いる理由の説明 にもなる。ビーム径を大きくすることでビームの発散を逆に減らすことができるためである。
ビームウエスト領域でのビーム径の変動は,次式によって定義される:
ガウシアンビームのレイリー領域は,ビーム断面積が 2倍になる地点のzの値として定義される。これは,w(z)が√2w0に増加した時に起こる。式(1-5)を用いて,レイリー領域(zR)は次のように表される:
これにより,w(z)をzRの関数としても表すことができる:
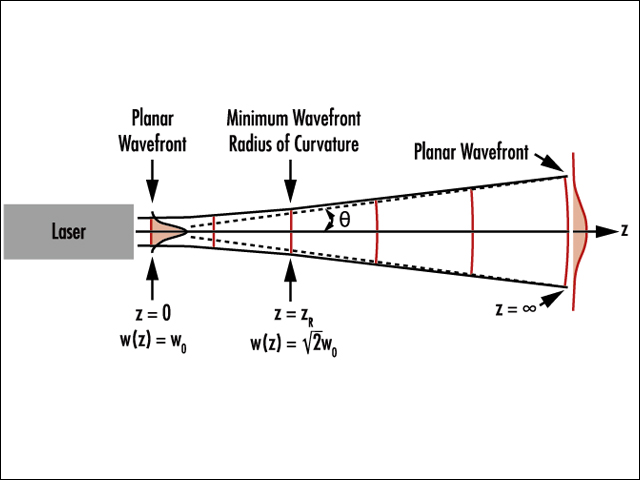
レーザーの波面は,ビームウエストでは平面状で,ビ ームウエスト領域から離れるに従い,再度この形状に近づく。これは,波面の曲率半径の大きさが無限大に近づき始めるためである。波面の曲率半径は,ビームウエストでの無限大をとり,そこから離れるに従い徐々に減少してレイリー領域で最小値をとり,そこから更に遠くに離れると無限大に戻っていく(図3)。これは,ビームウエストの両側について言えることである3)。
参考文献
1) Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia. html.
2) “Gaussian Beam Optics.” CVI Laser Optics, IDEX Optics & Photonics.
3) ÓShea, Donald C. Elements of Modern Optical Design. Wiley, 1985.
■Gaussian Beam Propagation 1
■Edmund Optics Japan Co., Ltd.
<お問合せ先>
エドモンド・オプティクス・ジャパン㈱
TEL: 03-3944-6210
E-mail: tech@edmundoptics.jp
URL: www.edmundoptics.jp