4. 反射と屈折

この章では,幾何光学の基本的な法則である,反射の法則と屈折の法則を説明し,前章で解説した光線追跡の手法により,それらによる光の伝搬を計算する。
4.1 正反射と乱反射
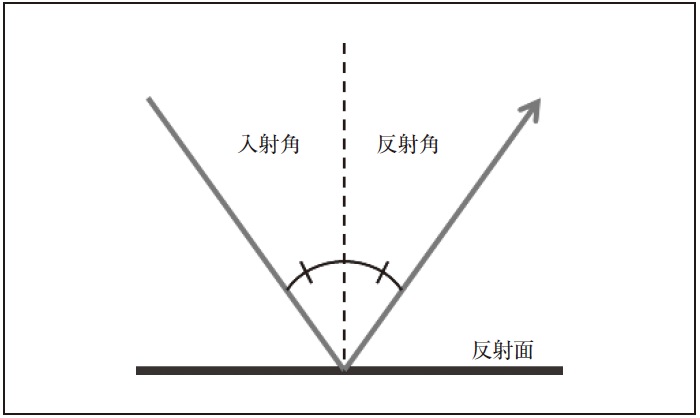
光が物体に入る時,その光の一部は,必ず反射する。この時,物体の表面が鏡面のように滑らかな場合,図2.10に示すように,光は一方向に反射し,正反射と呼ぶ。物体の表面に垂直な法線を引き,入射光線とこの法線のなす角度を入射角とすると,光線は,入射光線と法線を含む面内で,法線に対して,入射光線と対称な方向に反射する。この時,反射光線と法線がなす反射角は入射角と等しくなり,これを反射の法則と呼ぶ。通常の物質の表面は,鏡のように滑らかであることは稀で,細かい凹凸がある。このような凹凸がある場合には,それぞれの凹凸に対して反射の法則にしたがって反射するので,トータルで考えると,拡がった範囲に反射する。このような反射を乱反射と呼び,乱反射により,物体は,いろいろな角度から見ることができる。
この続きをお読みになりたい方は
読者の方はログインしてください。読者でない方はこちらのフォームから登録を行ってください。