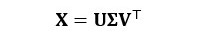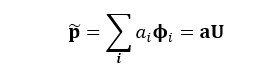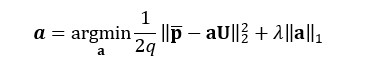1. はじめに
航空機,鉄道車両の空力設計において,飛行時・走行時の機体・車体の周りの空気の流れを適切に把握することは重要性が高い。特に物体表面に生じる圧力分布を知ることは非常に重要である。近年では,計算機の性能向上に伴い数値シミュレーションによる空気流の解析が行われるようになってきているが,流動挙動は非常に複雑でシミュレーションだけで解決できる問題は限られており,実験による現象把握の重要性は非常に高い。物体表面に生じる圧力を計測する手法として,計測対象に小さな孔(圧力孔)をあけ,これにつないだ半導体圧力センサーで圧力を測る方法が広く用いられている。
この手法では圧力孔を設置した位置での圧力を高精度に計測することができる一方で,予め圧力孔を設置した位置での点計測に限定されてしまう。近年,感圧塗料(Pressure-Sensitive Paint)計測法1, 2)と呼ばれる光学的な圧力計測法が大きな注目を集めている。PSP計測法では,酸素消光作用を有するりん光分子をこれを保持固定するための高分子バインダとともに計測対象に塗布する。この塗布された膜をPSPと呼ぶ。
PSP(に含まれるりん光分子)に励起光を照射した際に発せられる発光の強度が,酸素消光作用によって圧力に応じて変化する3)ことを利用し,PSPの発光強度変化を計測することで圧力を算出するというのがPSP計測法の原理となる。PSP計測法では,発光強度分布をカメラで撮影することで,PSPを塗布した面の圧力分布を計測することができ,従来の圧力孔による計測に対して優位性を持つ。また圧力孔が設置できないような小さな対象,半導体圧力センサーの配線が困難な回転体の圧力計測などは非常に有効であり,著者らもこれらを対象とした計測を進めてきた4, 5)。
PSP計測法はこのような利点があるものの,発光強度の変化を検出するために微小な圧力変化の検出は不得手という欠点があった。例えば,大気圧近傍(100 kPa)での1 kPaの圧力変化を検出するためには,0.7%程度の発光強度の変化を捉える必要があり,この変化はしばしばカメラのショットノイズと同程度である。定常な流動場では,複数枚の画像をとり加算平均することでショットノイズの影響を低減できるが,非定常な流動場の計測では加算平均ができず,他の手法によってノイズ減算を行う必要がある。大気圧近傍での1 kPaオーダーでの圧力変化は多くの機器において現れるため,現在主に航空工学の分野に限定されているPSP計測法の適用範囲を拡大するためにノイズ減算手法に関して非常に盛んに研究が行われている。
例えばYoritaらは,周期的な流れに対して,圧力孔で計測した時系列の圧力データを基準信号とし各位相毎に画像平均を行うことでノイズ減算を実現している6)。他にも著者らにより,やはり周期現象を対象に,ヘテロダイン法を利用することで対象とする周波数の信号を効果的に取り出す手法が提案されている7)。
2013年以降,特異値分解(Singular Value Decomposition;SVD)/固有値直交分解(Proper Orthogonal Decomposition;POD)8, 9)や動的モード分解(Dynamic Mode Decomposition;DMD)10, 11)などを利用した手法が提案されるようになった。SVD/PODは比較的簡単に実装でき,またノイズ減算が効率的に行えるため非常に有力な方法である。これらの手法では,撮影されたデータをモード分解したときに,低次モードが主要な流動現象を表現し,高次モードにノイズが含まれていると考え,低次モードだけを残して圧力分布を再構成することでノイズを低減する。しかし,どのモードまでを低次モードとして残すのかというところに任意性があった。そこで著者らは,スパースモデリングを用いて圧力分布を表現する手法の提案を行っている12)。
2. PODモードとスパースモデリングによる圧力分布再構成法
ここでは簡単に著者らの提案した手法を紹介させていただく。詳細は著者らの論文を参照いただきたい12)。 PSP計測によりN個の時系列データとして圧力分布データp1, p2, …, pNを取得する。これらはカメラで撮影しているために2次元の行列形式のデータになっているが,これらをそれぞれ列ベクトルになるように並び替えを行い,それを改めてp1, p2, …, pNと表記する。このN個の列ベクトルを横に順に並べた行列Xを考える。すなわちX=[p1, p2, …, pN]とする。これは
のように左特異行列U,右特異行列V及び対角成分に特異値を降順に並べた対角行列Σを用いて分解することができる(特異値分解)。ここでTは転置を表す。ここで左特異行列Uの各列がPODモードと呼ばれ,i番目のPODモードをφiと書くときU=[φ1, φ2, …, φN]となる。ここで1からr番目(r < N)までのPODモードから圧力分布を再構成するのが従来の手法8)であり,rの決定に任意性があった。本手法では,使用するPODモードの選定をスパースモデリングの枠組みで決定する。PODモードを用いる場合,再構成される圧力分布p~(~はpの上。以下同。)は各PODモードに対する重みaiを用いて
と書ける。ここでaは重みaiを並べたものである。このようにして表される圧力分布p~が目標となる圧力分布p-(-はpの上。以下同。)に近くなるように
として重みaを決定する。ここで||α||kはαのlkノルムを表し,λ は10分割交差検証によって決定される値を中心に3つの場合を試した。これはよく知られるLASSO(least absolute shrinkage and selection operator)回帰13)となっており,重みaがスパースであるとしている。
言い換えると少数のPODモードで現象を表現することで,従来手法の任意性をなくしている。目標値となる圧力分布p-として,本研究ではセンサー位置最適化問題によって定められる空間位置における計測データをフィルタリングして用いた。ここで適切なセンサー位置を抽出することはノイズ除去能に直結するため,重要なプロセスであり,貪欲法14)をはじめ複数の手法を検討・提案している。詳しくは著者らの論文12, 15)を参考いただきたい。
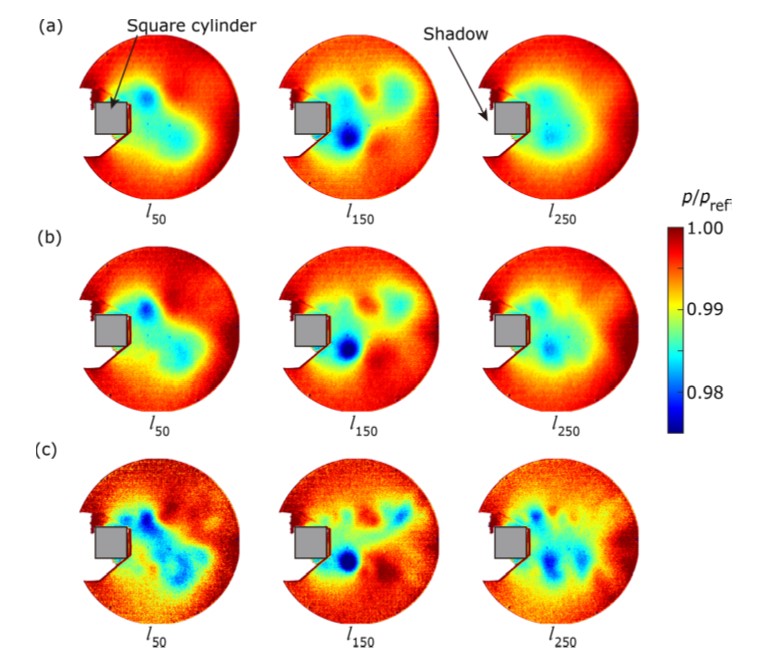
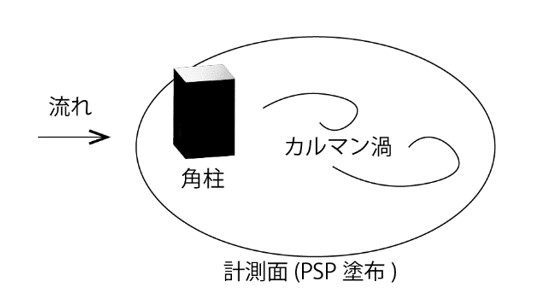
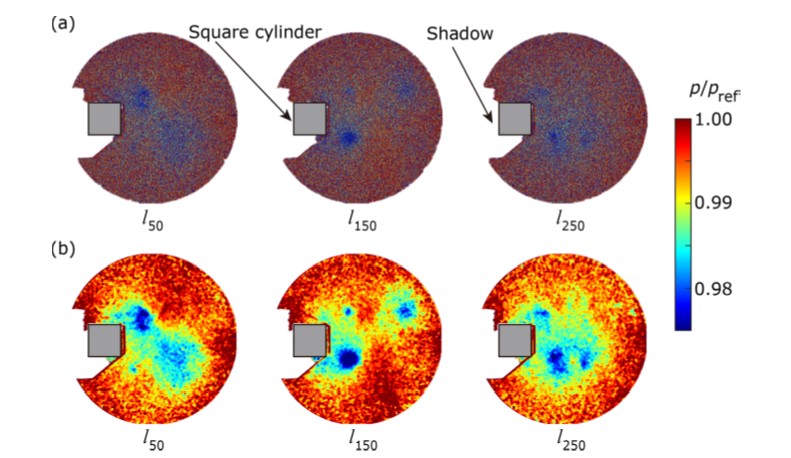
著者らの論文では,角柱後方に生じるカルマン渦(図1参照)によって生じる圧力分布の計測データに対して提案手法を検証している。図2に生データと一般によく用いられる空間フィルタリングを施したデータを示す。生データから圧力分布は非常に大きなノイズを含んでいることが分かる。また空間フィルタを施したデータでは渦の様子が確認できるが,空間分解能が大きく低下している様子も確認できる。また依然としてノイズも含んでいる。図3にデータ処理後の圧力分布を示している。