2.　計算機ゴーストイメージング

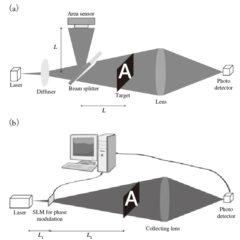
スペックル照射分布を用いたゴーストイメージングおよび，計算機ゴーストイメージングの計測系概略を図1に示す。まず，図1（a）に示すゴーストイメージングの計測手順について説明する。光源から射出されるコヒーレント光が散乱体を通過し，伝播することで測定対象においてスペックル分布が照射される。

この際，測定対象に照射する信号と等価なスペックル強度分布をイメージセンサーで記録する。散乱体を回転させる等で，照射分布を変更し，受光素子とイメージセンサーにより信号を記録する。数千回の計測を行い，得られるデータセットを用いて画像再構成を行う。

測定対象における（x, y）画素の強度透過率をT（x, y）とおくと，

⑴

で表される。この式において，B_i は測定i（i =1, 2, …, n）における受光素子の強度データである。I_i（x, y）は照射散乱光の強度分布であり，イメージセンサーで取得したデータを用いる。<>は全測定の平均を表す。式⑴は，スペックルの2次統計に基づく相関関数と計測モデルから導出される式である。

ゴーストイメージングの特性としては，微弱光照射で画像情報を取得できることが指摘されている。文献4）において，X線計測を低侵襲で行うためにゴーストイメージングを用いる手法が報告されている。

ゴーストイメージングにおける照射光分布の計測を計算機シミュレーションで代用する手法が図1（b）に示す計算機ゴーストイメージングである。図より，散乱体の代わりに，光波の位相分布を操作できる空間光変調器（SLM; Spatial Light Modulator）を用いる。変調器において，光波をランダム位相変調させ，光を散乱させる。式⑴に示すI_i（x, y）を，位相分布とSLMと測定対象の距離をパラメータにして計算機シミュレーションにより求める。SLMを必要とする理由は照射分布を求めるために既知の散乱特性が必要であるためである。スカラー回折理論に基づく光伝播により照射強度分布を計算することが可能である。

計算機ゴーストイメージングは，イメージセンサーを全く必要とせず，計測系を簡便にできることから，ゴーストイメージングの実用性を向上させるうえで重要な提案といえる。

一方で，1000回以上の計測を必要とすることと，空間光変調器のリフレッシュレートを考えると，計測対象が静止物体に限定されてしまう。計算機ゴーストイメージングにおいて，その高速化は重要な研究課題のひとつといえる。