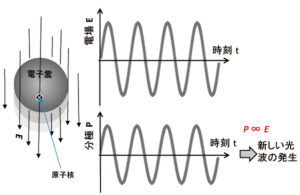
もう一つの空間コヒーレンスに話を移します。これは，光源内の異なる2点における光波の関係によって表されます。たとえば，放電管などの光源においては，各点から出てくる光波は互いにランダムな位相関係にあり，空間コヒーレンスは極めて悪いと言えるでしょう。各原子から出てくる光は10^-9秒程度のコヒーレンス時間を持っていますが，異なった原子から出てくる光には一定の位相関係がなく，空間的にはインコヒーレントです。

レーザーの場合は，誘導放出を利用して光を出していますので，各原子から出てくる光の間には一定の位相関係があり空間コヒーレンスは良いのです。

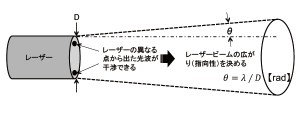
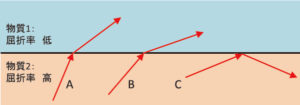
空間コヒーレンスは，光源から出てくる光線の平行度（指向性）および集束度に関係します。しなしながら，たとえコヒーレント光源であっても，完全に平行なビームが得られるわけではなく，図4のようにビーム広がりを生じます。このビーム広がり角θはλ/D [rad]で与えられます。ここで，λは波長，Dはビーム直径です。

例えば，2ミリラディアン（mrad：角度の単位で180°＝πrad（ラジアン））の発散角を持つレーザー光線が10 m離れた地点の壁に当たったとき，壁の上での光線の大きさは10×0.002=0.02 mだけ広がり，光線の直径は0.04 m，すなわち4 cmとなります。このように発散角が小さいことは，レーザー光線（ビーム）が一方向に向かつて線のように進むことを意味しており，レーザーの持つ特徴の一つとなっています。

さらに，ヘリウムネオンレーザーのビーム径が1 mmのとき，λ/D＝6.33×10^-4 [rad]となります。このレーザー光を50 km離れたスクリーンに照射すると，この地点におけるビーム径は30 mとなります。ところで，もし，このビームを100倍の望遠鏡を使って直径が100 mのビームに変換すると，λ/D＝6.33×10^-6 [rad]となり，50 km地点におけるビーム径は30 cmと小さくなります。