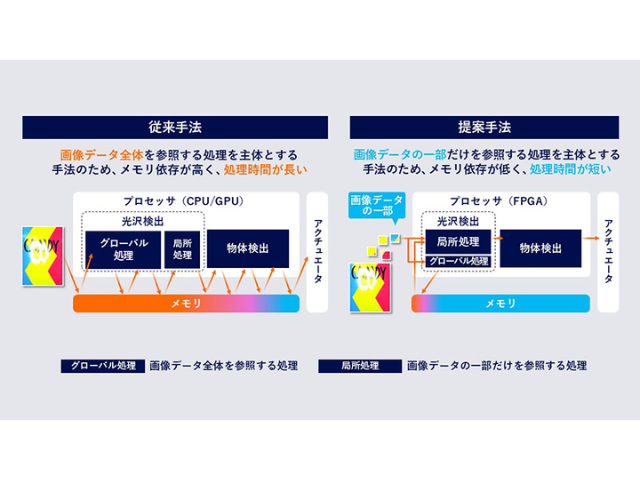
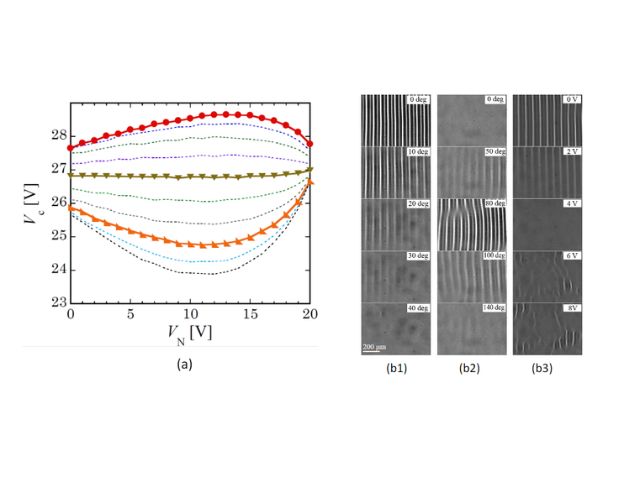
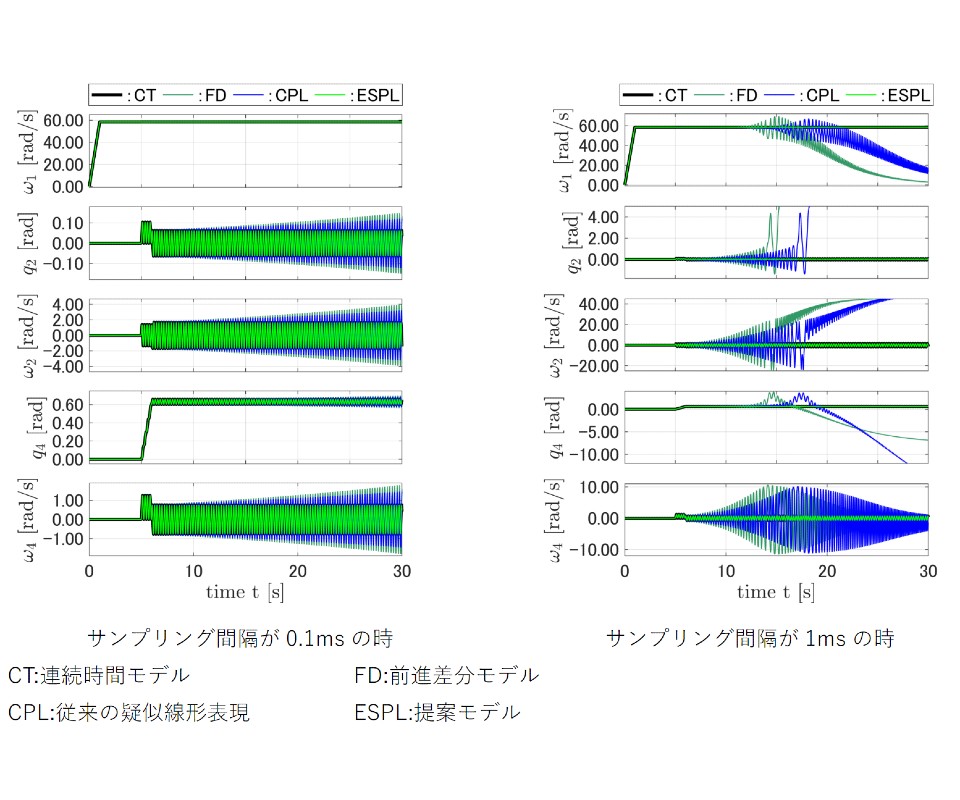
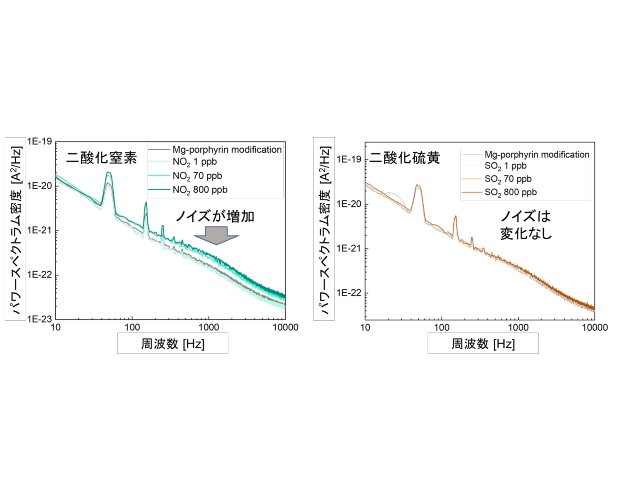
 東北大学の研究グループは,ノイズのある計測データからでも力学系のラグランジアンを獲得し,その運動方程式の解析的モデルを獲得可能であることを示し,データのみからプロキシマル勾配法を用いてスパースなラグランジアン表現を得ることを実証した(ニュースリリース)。
東北大学の研究グループは,ノイズのある計測データからでも力学系のラグランジアンを獲得し,その運動方程式の解析的モデルを獲得可能であることを示し,データのみからプロキシマル勾配法を用いてスパースなラグランジアン表現を得ることを実証した(ニュースリリース)。
未知のデータから物理法則を獲得する試みはこれまで長く行なわれてきた。ニューラルネットワークを用いたブラックボックスモデルによるアプローチは近年も継続して行なわれているが,入出力関係しか明らかにならないという根本的な問題がある。
非線形力学のスパース同定(SINDy)が近年提案され,陽に解析的方程式を導くホワイトボックスのアプローチとして注目されている。しかしながら有理関数への対応やデータノイズに対する頑健性が問題視され,その問題点を改良したバージョンが2020年に発表されている(SINDy-PI)。
これにより以前のものより有理関数対応の側面では改善されたが,実世界の測定データ活用に向けたノイズへの頑健性については,まだ十分に問題が解決されていない状況だった。
研究ではSINDyの概念を取り入れながら,プロキシマル勾配法を用いてスパースなラグランジアン表現を得ることを可能とした新しい計算手法により,ノイズへの頑健性のある非線形力学のスパース同定法(xL-SINDy)を提案した。
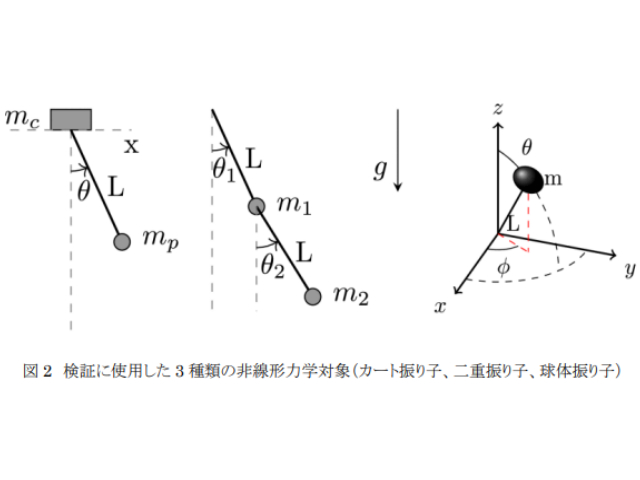
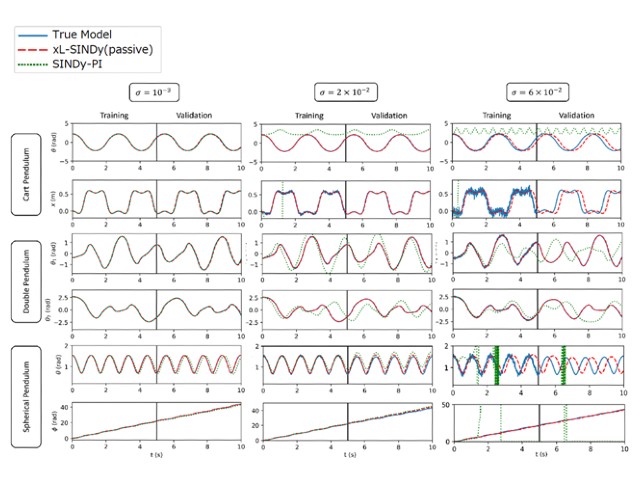
4つの異なるダイナミクスをもつ機械システムを用いて,異なるノイズレベルに対して提案手法の有効性を実証した。さらに,SINDyの最新のバージョンであるSINDy-PIと比較し,有理非線形性を取り扱うことができることを示した。
その結果,ノイズを含むデータから非線形力学系の支配方程式を直接抽出するため,既存の方法よりも一桁大きいノイズに対して頑健であることが明らかになった。この成果は,未知のデータから物理法則を抽出するためのデータノイズに強い計算法開発に向けた重要な貢献であるとしている。
ビッグデータや機械学習の発展から今後もますます実験データから得られる時系列データをモデリングする手法のニーズは高まっていくと考えられる。ニューラルネットワークを用いたブラックボックスにより近似モデルを推定する手法が盛んだが,入出力関係のみの推定となり解析的に用いることができる用途は限られる。
この研究では対象の力学方程式をホワイトボックスとして獲得できるため,非線形力学解析および「説明可能な AI」技術に貢献しうるとしている。この研究はエネルギー保存系での実現であるため,今後エネルギー散逸系での実現が期待されるという。また今後はブラックボックスとホワイトボックスの両アプローチの融合が望まれるとしている。