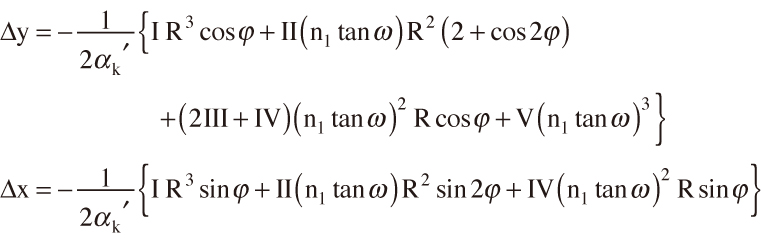4.3　収差各論

収差が数式的にどのように分類されるかについては明確になった。本章では，主要と分類された幾つかの収差がどのような性質を持っているかについて個別に説明する。

4.3.1　収差の式の展開

Seidelの5収差は光軸対称性を持つ結像の式を展開していった時に近軸に続いて現れる最初の次数の項を分類したものである^1）。どのようなパラメータが収差に効くのかを理解するため，基本となる5収差の式の表現を見てみる。式を見ただけでも各収差について多くを知ることができる。

Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴを3次の球面収差，コマ収差，非点収差，球欠像面湾曲，歪曲を表わす収差係数とする。横収差はⅠ～Ⅴを用いた式⑻で表わされる^2）。Rとϕは主平面の極座標表示，ωは像高に対応する主光線の画角である（図6参照）。

⑻