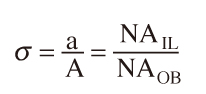3.6.3.3 パーシャリーコヒーレント結像
前章ではコヒーレント結像での点光源の特性を解析した。光源の位置,物体の空間周波数sによって光学系を通過する様子は大きく変わる。点光源の位置をずらしながら点数を増やしてインコヒーレントに重ね合わせると最終像が形成される。この像の解析を行うのがパーシャリーコヒーレント理論である。
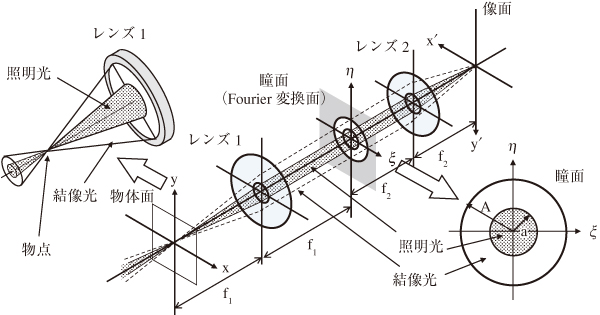
解析のため,光学系の回転対称性を考慮してcoherence factorと言われるパラメータσを導入する。図33は図22の再回折光学系にσを追記したものである。瞳面での結像光の半径をAとし,同じく照明光の半径をaとした時,σは式(50)で表わされる1)。
σは結像光と照明光の角度比である。像側の角度に対応するNA(n sinθ)がNAOB,0次光に相当する照明光のNAがNAILである。瞳面上での照明系の0次光の分布は有効光源と言われる。σの値は結像性能を変化させるだけでなく,光源の数が増えるので照明光量にも影響を与える。
コヒーレントの場合と同じくコントラスト1の正弦波グレーティングの像面強度分布を考える。有効光源内の強度分布は一様とする。ケースA~Dの強度分布は式(43)~式(45)で求まっており,ピーク値は表3で表わされる。理想結像では光源の位置によらず,像面強度分布のピークの位置ずれがない。従って,ピーク値に有効光源内の対応する光源の面積をかけて足し合わせればトータルの強度分布,及びコントラストが計算できる。より精密には光線の傾きファクタを考慮しなければならないが,ここでは0次近似として同一の寄与とする。
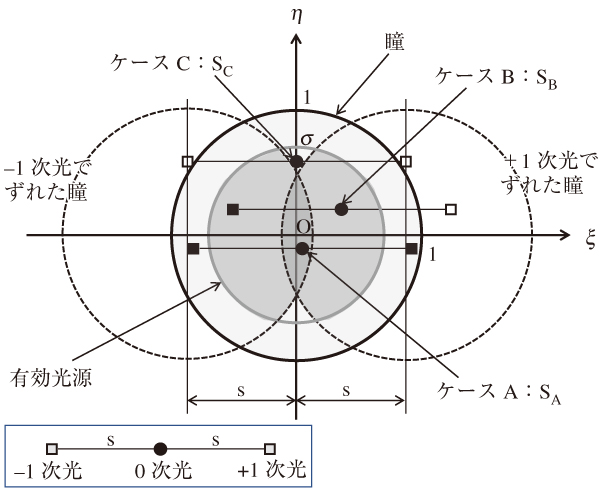
図34はσ 0.7,s 0.9の場合の瞳面の様子である。半径0.7の有効光源内の各点は回折光の着地する位置によってケースA~Cに分割される。回折光が瞳の外に出たかどうかは±s(この場合は0.9)ずらした単位円を有効光源に重ね描きすることでチェックできる。図より半径σの有効光源内のA~Cの面積SA~SCを求め,表3と組み合われば,理想結像でのトータルの強度分布が計算される。なお,ケースDはσが1以上になった場合に発生する。
この続きをお読みになりたい方は
読者の方はログインしてください。読者でない方はこちらのフォームから登録を行ってください。