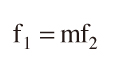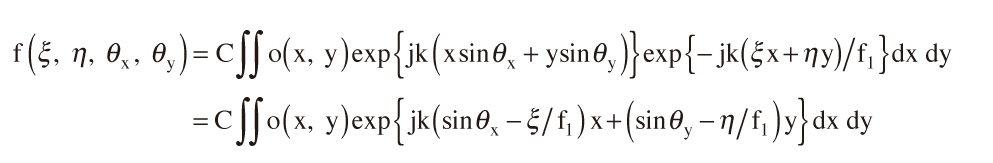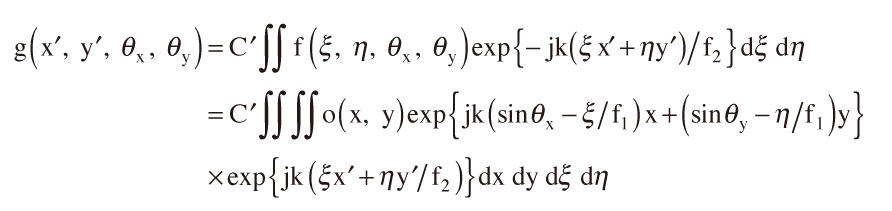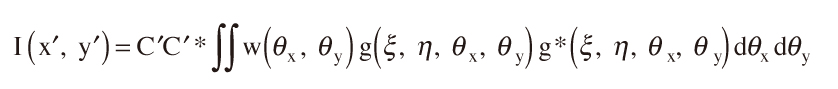3.6　コヒーレンス結像論

光が干渉性を持つ電磁波で挙動がsin，cosのような正弦波関数を用いて記述できることは素晴らしいことである。世の中には時間や空間で単純な経過や拡がりで記述される現象と時間軸の周波数や干渉縞の空間周波数の様に繰り返す周期現象がある。正弦波は最も基本的な周期関数である。

実際，一つの事象あるいは画像は空間座標と空間周波数座標の双方で等価な関係に表現することができる。どちらで表わした方が考えやすいかは場合によって異なるので，都度適切に選ぶと良い。本章ではこの概念の最も活躍する照明法の結像性能への影響，即ちコヒーレンス結像論を取り扱う。

3.6.1　再回折光学系

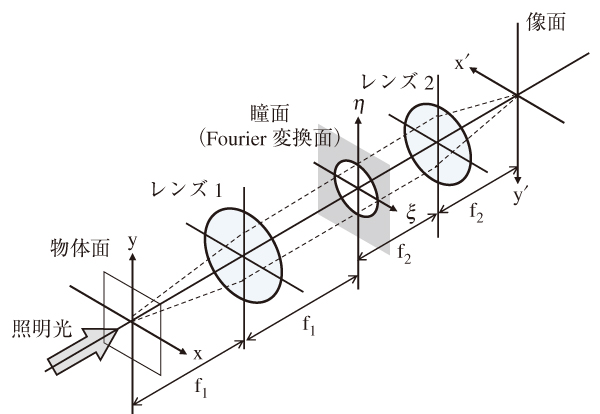
図22は再回折光学系という結像系で，結像の仕組みを解析する一般的な議論に適した構成になっている^1）。物体面，瞳面，像面がレンズ1，2の焦点位置にあり，いずれかの面に平行で入った光は次の面で結像し，更に次の面では再び平行光に変換される。顕微鏡や半導体露光装置の光学系では図22の構成を取るものも多い。物体と像面の座標の方向を逆に取ったので，光学系の倍率1/mは正の値となる。レンズ1とレンズ2の間が平行光なので，両者の焦点距離f₁，f₂は

(33)

である。図22はまた，物体面，像面ともにテレセントリックな構成でもある。

再回折光学系は物体からの角度分布が瞳面に反映されるFraunhofer回折で説明した構成で，物体面と瞳面，瞳面と像面がFourier変換の関係で結ばれる。

図22の結像を式に書くと式(34)のようになる。先ず，瞳面上での振幅分布f（ξ, η, θ_x, θ_y）は

(34)

θ_x，θ_yは物体を照射する角度分布，o（x, y）は物体の複素透過率分布を示す。図22に示したのはケーラー照明という最も一般的な照明法で，光源上の各点を出た光は平行になって物体を照明した後，瞳面に結像する。光源は準単色光とする。

像面の振幅分布g（x′, y′, θ_x, θ_y）はf（ξ, η, θ_x, θ_y）のFourier逆変換となり

(35)

最終的な強度分布はI（x′, y′）は

(36)

w（θ_x, θ_y）は光源の明るさ分布である。「最終的な像強度分布は光源の1点1点が作る強度分布を重ね合わせて計算される」というメッセージが重要で，これがコヒーレンス理論の根幹となっている。

式(36)は理想結像に対する式で収差W（ξ, η）がある場合は式(35)の積分内の関数に更に位相項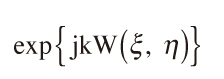を導入する。収差は後の章で論じるので，本章では理想的な結像状態での性能を取り扱う。