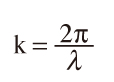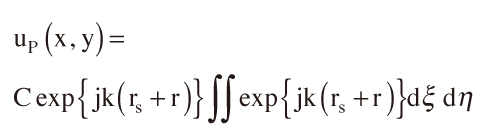3.4 Fraunhofer回折
3.4.1 回折パターンの計算
R. P. Feynmanが量子電磁力学を一般向けに論じた本でミラー反射を取りあげている1)。説明ではミラーからは正反射を行う部分だけでなく,あらゆる位置を通る経路で光子が来ており,その積分効果として反射現象が成立することが示される。あらゆる位置を通っている例は回折格子で,ミラーを部分的に隠して境界条件を変えた途端にそれまで存在しないと思われていた新しい光路が出現することがその証拠である。即ち,色々な経路を通る光子が存在する。
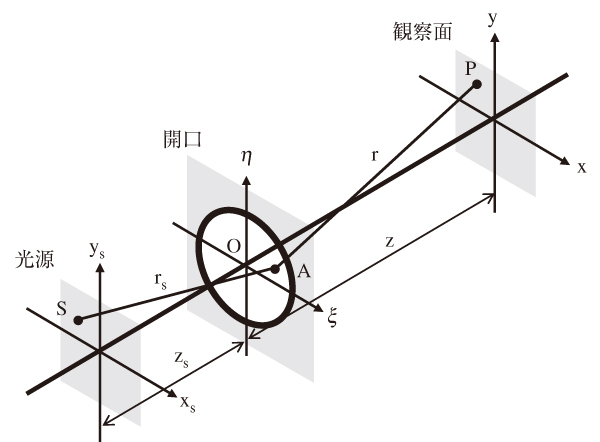
光学系を構成する素子間であらゆる光路が存在することを念頭に,回折現象を扱ってみる。図14に計算座標を示す。光源座標を(xs, ys),開口面を(ξ, η),観察面を(x, y)とする。
回折現象の厳密な扱いは光伝播の際の指向性であるinclination factorの考慮から始まるが,ここではその検討後から出発する。光は正弦波として扱える。1波長進むと位相は2π進むので,伝播に伴う光の位相変化を計算する波数kを通常のように
と定義する。光源上の点Sから,開口部(パターン部)を介して観察面Pに与える振幅分布uPは開口部からの影響を積分して
と表わすことができる。rs,rはそれぞれ光源~開口,開口~観察面の距離,Cは定数である。
この続きをお読みになりたい方は
読者の方はログインしてください。読者でない方はこちらのフォームから登録を行ってください。