慶大ら，量子もつれに変化をもたらす新条件を発見

慶應義塾大学と理化学研究所は，量子もつれと量子測定の強さの競合によって生じる量子測定誘起相転移が発現するための新たな条件を発見した（ニュースリリース）。

量子力学的な時間発展には，放っておくと量子もつれを増大させていく性質がある。

一方，量子多体系の各部分を，頻繁に量子測定していくと，量子もつれを増大させる量子力学的時間発展の効果と，量子測定によって状態変化を阻害する効果との間に，ある種の競合が生じると期待される。

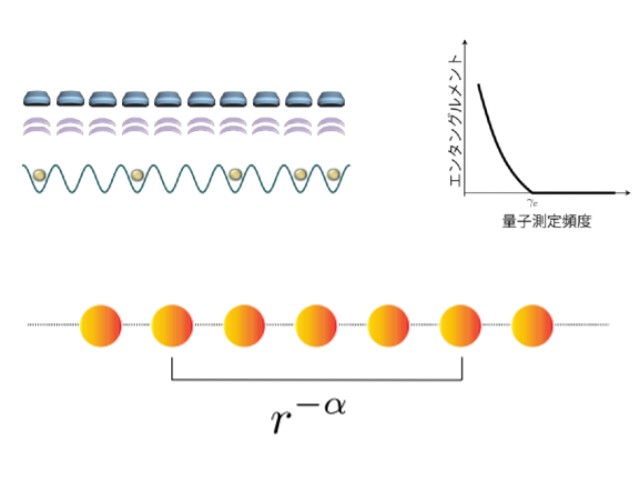
量子測定の頻度を増やしていくと，ある頻度で量子もつれの増大率が変化しなくなる相転移現象が生じることが分かる。このような相転移現象は，近年「測定誘起相転移」現象と呼ばれ，活発に議論されている。

この相転移現象の主な研究対象は，隣接する相互作用のみを考えた量子回路を使った系だった。そのため，一般的な系においてこの現象がそもそも発現するのか，そして発現するとしたらその特徴をどう捉えることができるのかなどの課題は未解決だった。

そこで研究グループは，これまで研究されてきた短距離の相互作用のみがはたらく系を超えて，長距離にもはたらく相互作用系を考えた。自然界には，重力や電子間にはたらくクーロン力など，遠くまで到達する力がたくさん存在し，そのような力を長距離力と呼ぶ。

一般に長距離力のポテンシャルは，距離?の関数として 1/?^?で表現される。近年の冷却原子系の実験的な進展により，長距離力のパラメータ?を自在に制御することが可能になってきた。長距離力がある系では瞬時に二つの粒子が影響し合うことができるため，量子もつれは短距離相互作用系よりも増大してしまいそうに見える。

研究では長距離力をもつ量子多体系において，測定誘起相転移現象が発現する条件を考察した。?次元の長距離相互作用系を考え，量子もつれの成長率を解析することにより，測定誘起相転移現象が発現する十分条件を求めた。

系のハミルトニアンが2次形式で表される系では，?>?/2+1が条件となり，それ以外の一般的な系では，?>?+1が条件になることを見出した。またこれらの条件は，1次元系において，大規模な数値計算によって確かめた。

この研究のように高次元系での発現条件を簡潔な式として示した例は他になく，この条件を高次元系において，数値計算などで確かめることが今後の課題となるという。

また，この研究での量子測定とは，典型的な量子散逸として捉えることができる。これについて研究グループは，量子コンピューティングにおける，量子もつれへのノイズの効果を理解する上で，様々な示唆を与えることが期待されるとしている。