高輝度光科学研究センター（JASRI）は，繊維状試料のX線回折像から，繊維の実空間3次元微細構造を復元する方法を提唱した（ニュースリリース）。
X線や可視光などの光（電磁波）や電子線を物体に照射すると散乱が起こる。その散乱は，数学的には物体の構造のフーリエ変換になる。その散乱をもう1回フーリエ変換すると（逆フーリエ変換），もとの物体の構造を復元することができる。
これが実際に光学顕微鏡や電子顕微鏡の原理で，逆フーリエ変換の機能はレンズが担っている。これらの顕微鏡の分解能は，使う電磁波や電子線の波長と同程度となる。X線の波長は0.1nm，つまり原子1個の大きさと同程度なので，X線を使う顕微鏡があれば，原子の1つ1つを観察できると期待される。
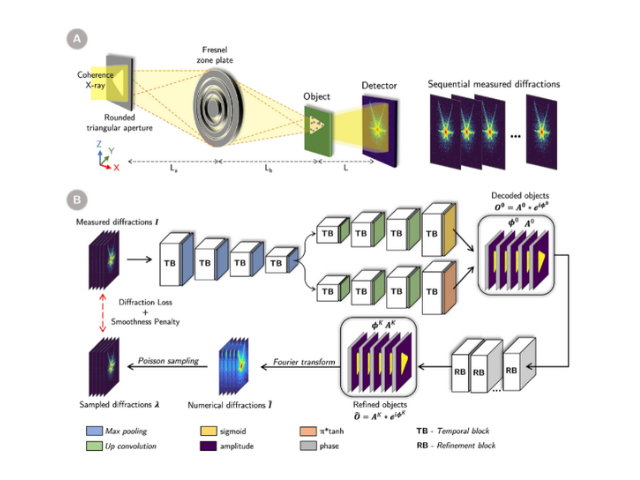
しかし，X線では光学顕微鏡のようなレンズが作成できないため，通常は物体によるX線の散乱（回折像）を検出器に記録して，それを直接解析するという手段がとられる。だが，X線の散乱の振幅と位相のうち，検出器で記録できるのは振幅だけで位相は失われてしまうため，逆フーリエ変換しても元の構造は復元できない。
しかし計算技術の進歩によって，失われた位相情報を回復して物体の構造を復元する方法が考案されており，コヒーレント回折イメージング法（CDI）はその1つ。CDIは金属ナノ粒子のようなコントラストの高い孤立物体に対して有効で，また連続物体であってもCDIの応用であるタイコグラフィーで対処できる。しかし炭素のような軽元素が主体の繊維状試料の集合体に対しては，これまで適切な位相復元法がなかった。
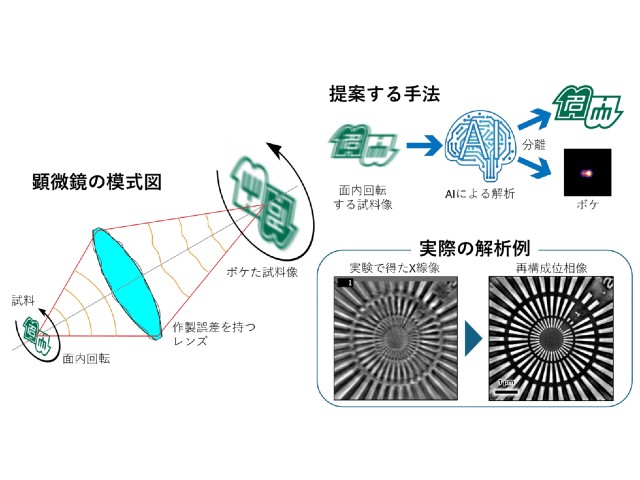
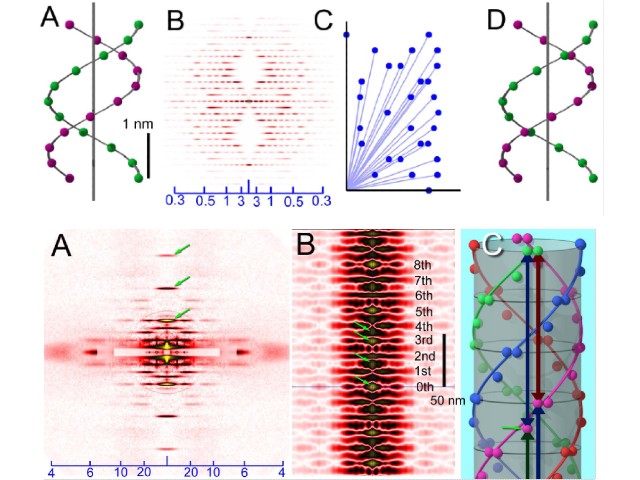
今回提唱した方法は，X線回折像から計算されるパターソン関数を利用したもの。パターソン関数とは試料に含まれるベクトルを網羅したもので，これらのベクトルを一定のルールの下でつなぎ換えることで3次元構造を復元する。
多くの繊維状試料では，構成する繊維が回転方向にランダムな向きをしているため，記録されるX線回折像も回転平均化されてしまう（円筒平均化パターソン関数，CAP）。この方法はCAPから，繊維の回転平均化されない3次元構造の復元ができる。研究ではマルハナバチ飛翔筋のX線回折像からCAPを計算し，そこからミオシン繊維の3次元構造を求めた。
今後は不完全なCAPから，正しいピーク位置を推定することが課題であり，人工知能の活用が期待されるという。さらにCAPのピークの広がりも利用すれば，密度分布を含んだより完全な3次元構造を求められるかもしれず，研究グループは，繊維状物質の3次元構造を調べるための重要なツールになるとしている。
