東京大学は，マヨラナ粒子の数学的構造を用いて，広いクラスのSU(N)引力ハバード模型の基底状態の基本的な性質を厳密に明らかにした（ニュースリリース）。
SU(N)引力ハバード模型は，複数の色の自由度をもつ粒子たちが互いに強く引かれ合う物理系。ハバード模型とは，元々固体中の電子の運動を記述するために導入されたモデルで，現在でも熱心に研究されている。
電子のスピンは，上向き，下向きの2つの自由度を持つ。ここでは，この自由度を「色」の自由度だとする。この色の自由度がN=2の場合が元々のハバード模型に対応し，これをN（= 3,4,5,…）色に増やし，粒子間に引力的な相互作用がある場合がSU(N)引力ハバード模型となる。
このモデルは近年，レーザー中にトラップされた原子によって実験的に実現されており，注目を集めている。色の自由度は，実験では原子の核スピンの自由度に対応する。このモデルでは，N色の粒子たちは以下の3つのルールに従って運動する。
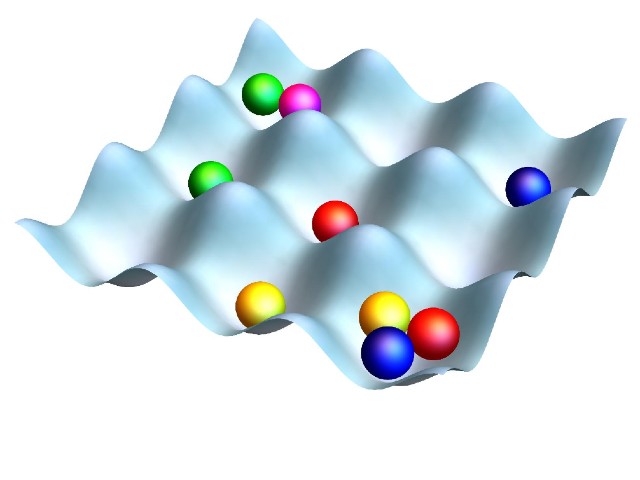
①粒子は格子上に存在し，格子上の点（サイト）の間を飛び移りながら運動する。
②同じサイトに同じ色を持つ粒子は2個以上存在できない（パウリの排他律）。
③同じサイトに（異なる色を持つ）複数個の粒子が来ると，引力によりエネルギーが下がる。
この物理系の解析は非常に難しい。その理由の1つに，粒子たちの取りうる配置が，サイトや粒子の数を増やしていくと爆発的に増加することがある。直接解かずに解析するためのアプローチとして，スピン鏡映正値性という数理手法を用いた方法があるが，このスピン鏡映正値性は上向きスピンと下向きスピンの対称性を用いた方法なので，色の自由度が2より大きな場合には適用できなかい。
そこで研究グループは，近年発見されたマヨラナ鏡映正値性という数理手法を応用し，広いクラスのSU(N)引力ハバード模型の基底状態の基本的な性質を厳密に示した。この手法を用いて，2部格子上のSU(N)引力ハバード模型の基底状態の数（縮退度）や，粒子数，さらに色の自由度を入れ替える変換に対して基底状態が不変であることを示した。また，2つの部分格子の上のサイトの数がマクロに異なるとき，系が電荷密度波的な秩序を示すことも明らかにした。
レーザートラップされた原子による実現を契機として研究が進むSU(N)ハバード模型は，新しい量子状態を示す可能性から注目を集めている。この研究はこの物理系の研究に関する新たな方向性を示し，さらなる発展を促すと期待されるとしている。
