東京大学は，XYZ模型と呼ばれる無数の保存量が存在するスピン系を解析し，それらの保存量の具体的な構造を明らかにした（ニュースリリース）。

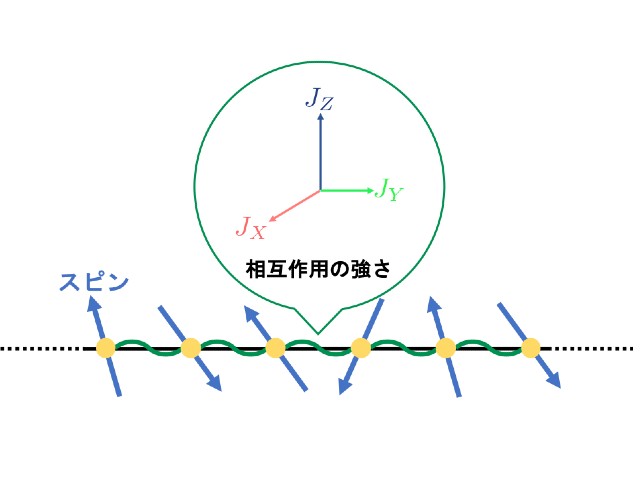
XYZ模型は1970年代にBaxterによって無数の保存量の存在が示されている代表的な可積分系の一つ。XYZ模型の単純な場合である，スピンにとって特別な方向がない（等方的な）場合に関しては，保存量の構造が先行研究によって明らかにされている。

しかし，異方性が存在するより一般的な場合に関しては，構造の複雑さのために等方的な場合における解決から25年以上の間未解決の問題として残されていた。

研究グループは，従来用いられてきた解析手法とは異なる，シンプルで初等的な手法を用いてこの問題を解決した。研究では，XYZ模型における保存量の構成要素を，それを特徴付ける「幅」と「穴の数」によってそれぞれのクラスに分類し，その構成要素がどのような比率で含まれるかをいくつかの保存量について調べた。

その計算の結果，構成要素の比率がある規則性に従っていることを発見した。この規則性に従うことで保存量に含まれる全ての構成要素の比率を定めることができる。そして，その規則性が無数の保存量において一般的に成り立つことを厳密に示した。

さらに，その規則性を用いて全ての構成要素の比率を具体的に求め，保存量の表式を明らかにした。この成果は，従来知られていた等方的な場合の結果を含めて一般的なXYZ模型に対して包括的に問題を解決したもの。

この研究によって，一般的なXYZ模型における保存量の具体的な構造が明らかになった。この表式は数値計算への実装が容易であるため，可積分系における非平衡現象を数値シミュレーションする際に応用されることが期待されるという。

また，この研究において保存量の構造が従う規則性を発見したが，この規則性と可積分性との関連性などの基礎科学的研究が発展し，保存量の数理的構造の理解がさらに進むことが期待されるとしている。

研究グループは，今回の成果を第一歩として，多数の保存量の理論的性質のさらなる解明を行ない，保存量を応用することによって非平衡現象の理解を進めていくとしている。