東京理科大学の研究グループは，トモグラフィーの効率と精度を向上させる新たな数学的手法を開発した（ニュースリリース）。
構造体の内側や地下など，見えないものを見るための技術の多くには，光や音波，放射線などの波の「散乱」によって得られる情報が使われている。研究グループは「逆散乱解析」と呼ばれる数学的な問題に取り組むことで，これまで見えなかった，見えにくかったものの構造をより効率良く再現しようとしている。
今回，ラメ定数（物体に力を加えたときの，物体の形の変化のしやすさを表す数）と質量密度が周囲から異なる領域を検出するための数学的な方法論を新たに展開した。この領域を点散乱源の集合で数学的に表現できると仮定することで複雑に分布する多数の点散乱源の位置を精度良く推定してイメージングを行なう。
音波などの波動が物体に入射するとき，これらの波は，物体内の散乱体と相互作用して散乱する。散乱波には散乱体の物理的な性質の痕跡が残されており，これを解析することで，対象となった物体の位置や特性を知ることができる。「逆散乱解析」とはこのような解析のこと。
散乱波を数学的に記述するためには「グリーン関数」が必要になる。グリーン関数はある特定の点で発生した波の振る舞いを，それとは異なる点で観測した結果を表す際に用いる。今回の手法では，まず，「最急降下法」を用いて新たに「擬似射影子法」を数学的に展開した。このようにしてグリーン関数から2点間の距離が一定以上離れた場合（遠距離場）の特性の情報を抽出した。
次に，近接場および遠距離場でのグリーン関数の特性を用い，散乱体の位置を決定するための指示関数を導いた。やや複雑な手続きだが，一連の流れの中で少数のセンサーで高精度にイメージングを行なえる数学的な手法を組み込んでいるという。
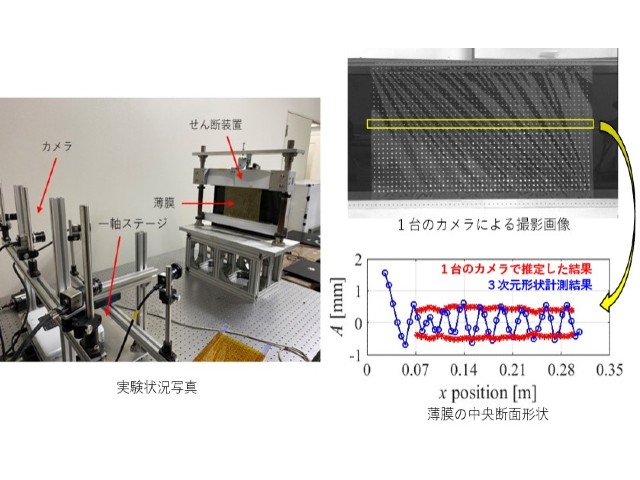
この理論的な枠組みを検証するために，送信センサーと受信センサーをグリッドの上に設定して，コンピュータを用いた数値的な実証実験を行なった。あらかじめ定義された物体の構造を参照入力（基準となる情報）として使用することにより，今回定義された遠距離場の演算子による指示関数で再構成した位置情報が，参照入力の情報と一致することを示し，少数のセンサーグリッドを使用して，密集した点散乱源の位置情報の再構成が可能であることを実証した。
今回の手法は，トモグラフィー技術の効率が高められる可能性があるほか，散乱体の複雑な分布によって特徴づけられる物体の構造のより精確なイメージングにも適用することが可能。将来的には，この理論を人体のイメージングにも適用できるように展開していきたいとしている。
