東京大学と米フラットアイロン研究所の研究グループは，機械学習の関数を用いた新たな数値計算手法を提案した（ニュースリリース）。

量子力学の法則に従う小さな粒子が互いに相互作用しあうような系を量子多体系と言う。例えば，電気抵抗が0になる超伝導現象や磁石を生み出す強磁性は，電子が互いに相互作用しあうことによって発現する量子多体現象。そのため，量子多体系の性質の解明は，身の回りの物理現象の説明に欠かせない。

量子多体系の性質は，量子力学の粒子が従うシュレーディンガー方程式（あるいはディラック方程式）の解である多体波動関数によって決定される。従って，多体波動関数がわかってしまえば性質がつまびらかになる。

性質解明のために，これまでに様々な数値計算手法が提案されてきた。しかしながら，系の自由度の数が増えていくにつれて，波動関数の次元が指数関数的に増大するため，一般には解析的に厳密な多体波動関数を得ることができない。そのため，数値計算によって，多体波動関数を精度よく近似する手法が様々に提案されてきたが，量子多体系の完全理解には未だ到達していない。

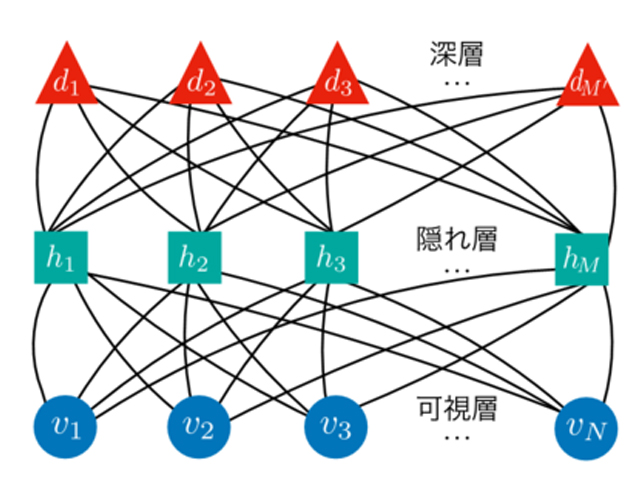
これに対し研究グループは，人工ニューラル・ネットワークの一種である深層ボルツマンマシンを用い，量子多体系の基底状態を任意の精度で表現できることを示した。得られた基底状態を表現する深層ボルツマンマシンをもとにして多体系の数値シミュレーションを行なうことにより，量子多体系の性質を調べる事ができる。系のエネルギーなどの物理的な性質は，得られた深層ボルツマンマシン状態をもとに数値計算によって求めることができるという。

この研究によって，高い関数表現能力を持つ機械学習の関数が量子多体波動関数の表現にも有益であることが示された。機械学習と物理という異なった分野間の交流により，今後ますます強力な数値手法開発につながっていくことが期待され，量子多体系に対する理解の促進にはずみをつける成果だとしている。