1. はじめに
従って,射出成形や延伸処理を施されたものは,ほとんどが複屈折を発現する。代表例の一つである延伸処理されたフィルムは複屈折を生じ,入射光に対して複屈折位相差を生じるため,液晶ディスプレイの位相差フィルムとして用いられ,今日普及した高精細ディスプレイを支えている。もちろん液晶材料自体も,結晶性を持つため複屈折媒体である。このほか,フィルムだけでなくファイバー状や板状に成形された場合等も複屈折を発現する。これらの複屈折媒体は,いずれも原子や分子が規則的に配列・配向した結果生じる結晶性に起因しているが,光波長よりも小さい周期性を持つ異方的な微細構造も,複屈折を発現し,「構造複屈折」と呼ばれる。
以上のように,私たちは複屈折を発現する媒体を活用して生活している。従って,様々な媒体の複屈折を簡便かつ正確に評価することは重要な技術的課題となる。ところが高度に発達したデジタル社会の現代においても,この複屈折の空間分布を高速かつ高解像で測定することは実は容易ではない。本稿では,筆者らが開発した回転操作不要の「2次元複屈折分布の高速・高解像イメージング技術」について説明し,実際に試作した複屈折プロファイラーによる様々な物質の複屈折観察や評価の例を示す。
2. 複屈折(位相差)の測定
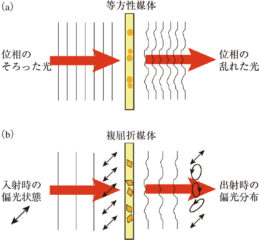
複屈折分布の測定は複屈折位相差の測定と同義的であるが,通常の位相差測定とは大きく異なる。図2(a)のように光が複屈折の無い等方性媒質を通過した場合には,生じる位相差も等方的に生じるため,参照光を用いることで干渉縞の縞解析から位相差分布を求めることができる。一方で,図2(b)に示すように複屈折媒体を通過した場合に生じる位相差は異方的に生じるため,複屈折位相差の測定は出射光の偏光状態を測定し,この結果に基づいて異方的に位相差を解析しなければならない。従って,複屈折の2次元分布の測定技術の開発は,偏光状態の2次元分布の測定技術の開発と言い換えることもできる。
一般的に知られているように,偏光状態の測定には,偏光子や検光子あるいは被測定物について,少なくとも180°以上の回転操作を行う必要がある。これは偏光状態の一般解が楕円であり,この楕円軌道を一つに決定するためには少なくとも3つの楕円半径を判別しなければならないことに起因している。これらの光学原理が,複屈折の2次元分布測定を難しいものにしている。この複屈折位相差の2次元分布測定において,上述の回転操作を省略することができれば,高速で高解像の複屈折分布測定技術の確立が期待できる。