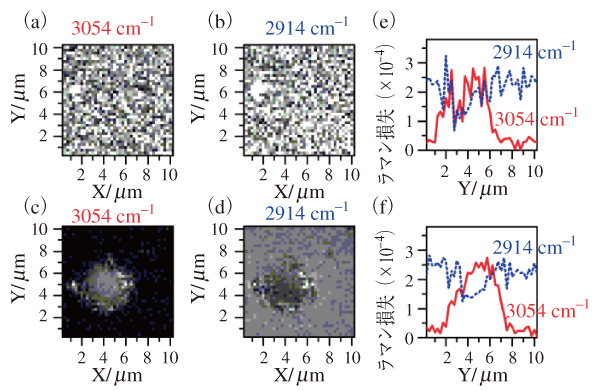
(a)と(b)従来法による測定でそれぞれPSとPVAのラマンバンドでイメージ,(c)と(d)位相検波法によるイメージ,(e)と(f)それぞれ位相の帰還制御が無い場合と有る場合
図8は誘導ラマンイメージングに適用した例で,試料はポリビニルアルコール(PVA)膜中のPS球である。図8(a)と図8(b)はそれぞれPSとPVAのラマンバンドに相当する3054 cm–1と2914 cm–1を従来法で同時に観測したものだが意味のある像が観測できない。図8(c)は3054 cm–1において雑音打消しを適用したもので,PS球が確かに観測できた。図8(d)は2914 cm–1のイメージであり,PVAの信号が,PS球に排除された部分で小さくなっている。
つまり,同時に多波数で強度雑音の削減と信号の観測に成功している。図8(e)と図8(f)はそれぞれ帰還制御無と有りの場合でX=4 μmにおけるY方向に平行な線上の信号である。赤実線はPS,青点線はPVAの信号を示している。図8(e)では,試料スキャン中にPS球上でaとbが変化するために雑音が現れている。しかし図8(f)では帰還制御によりPS球上でも常に雑音が削減されていることが分かる。
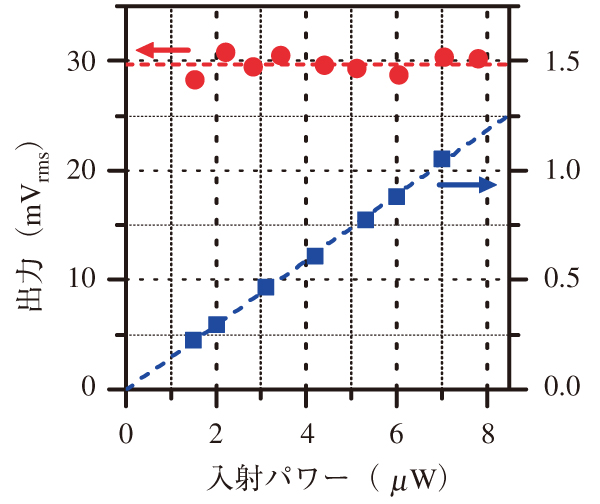
青四角点;光検出信号と光源同期信号との乗算結果,赤丸点;位相帰還制御信号,信号強度がプローブ光の強度に依存しないので雑音の乗算的な寄与が除去される。
ここで式⑸の第一行目に着目すると,φの帰還制御の応答速度をPuの強度変調よりも大きくしたとき,φは試料の強度変調mをも打ち消してしまい,図4(b)の出力1には何も現れなくなる。しかし,φはmに追従するように制御されるので,φの制御信号上にmと比例した信号が現れる(出力2)24)。mによる位相変調はAとは独立なので,φの制御信号にはAが現れない。従って,帰還制御の応答速度を大きくし,出力2を観測することでmに対する乗算的な雑音をも削減できる。その効果を示すのが図9である。横軸はPrとRfの平均入射強度で,縦軸はシクロヘキサンのラマンバンドによる信号強度である。青四角点は帰還制御を遅くした時の出力1,赤丸点は帰還制御を速くした時の出力2を示している。出力1は入射強度に比例していて,入射光の揺らぎ,強度雑音がラマン信号に対し乗算的に出力されることが分かる。一方,出力2は入射強度とは無関係であり,強度雑音の乗算的寄与をも削減されることが分かる。
なお,原理的には先述の比較器(CMP)で光検出信号をデジタル化するなどしてAを固定することでも雑音の乗算的寄与を削減できる。実際,通信で用いられる位相検波では一般的方法である。しかし,実際のCMPは入力から出力までにかかる時間,つまり出力の位相がAに依存するので(分散特性という),Aが大きく揺らぐ光学測定においては強度雑音が位相雑音に変換される。従って,CMPでAを固定するアプローチは失敗した。








































