北陸先端科学技術大学院大学（JAIST），伊国際先端研究大学院大学，仏ソルボンヌ大学は，第一原理量子モンテカルロ法のソフトウェア「TurboRVB」を利用し，世界初となる第一原理量子モンテカルロ法による固体周期系の格子振動計算（フォノン分散計算）に成功した（ニュースリリース）。
シュレーディンガー方程式は，物質の電子物性を記述するための基本的な方程式であり，ミクロなスケールを対象とする計算科学の研究は，この方程式を厳密に解くことを究極の目標としている。
シュレーディンガー方程式を実験値に依らず解く計算手法を，総称的に「第一原理計算」と呼ぶ。現在，最も普及している第一原理計算は，密度汎関数理論（Density Functional Theory:DFT）に基づく方法であり，凝縮系物理学分野において，数多くの成功を収めている。しかしながら，密度汎関数法は，交換相関汎関数の選択によって大きく予見が変わるという大きな問題点があり，より厳密な次世代の電子状態計算開発が望まれてきた。
「第一原理量子モンテカルロ法」は，モンテカルロ法を利用して多体シュレーディンガー方程式を解く手法であり，結果が交換相関汎関数に依存しない点などから，次世代の厳密計算手法として期待されてきた。
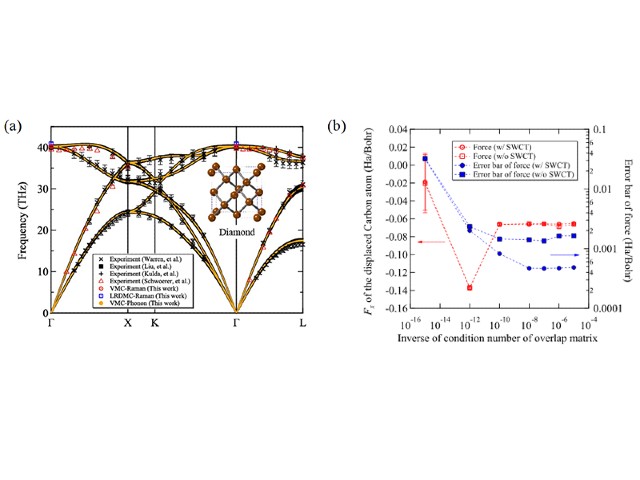
しかしながら，第一原理量子モンテカルロ法においては，厳密なエネルギー値は計算可能でも，その微分値（例：原子に働く力）の評価が容易ではないという問題が長年残されてきた。そのため，材料開発研究において重要になる安定構造の探索（構造最適化）や，格子振動（フォノン），自由エネルギー等の計算が出来ないことで，その応用範囲が限定されていた。
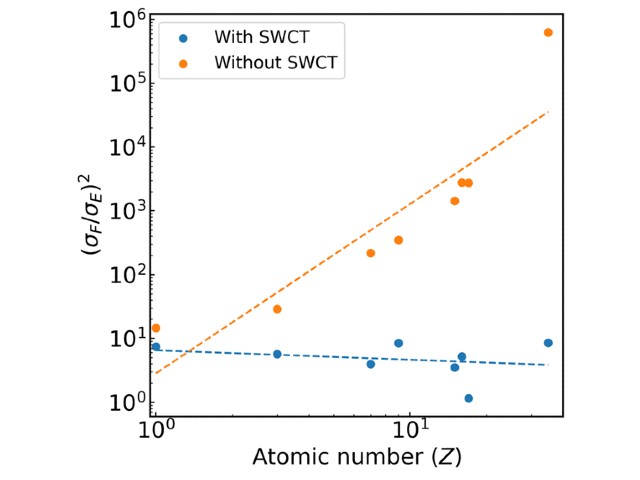
今回研究グループは，第一原理量子モンテカルロ法における，固体周期系での原子に働く力の評価値が持つ統計誤差発散の問題が，利用する基底関数の重なり行列の条件数，つまり，基底関数同士の線形従属性に起因することを発見し，その基底関数の重なりをうまく排除してやることで，これまで問題となっていた統計誤差の発散を劇的に抑えることに成功した。さらにその開発した手法を，参照系として典型的な物質であるダイヤモンドに適用し，実験値と一致するフォノン分散が得られることを確認した。
今回の成果は，これまで限定されてきた第一原理量子モンテカルロ計算の応用範囲の裾野を大きく広げるものであり，これまで計算材料科学が取り扱いに難渋してきた物質に対しても精度の高い格子物性計算を可能にする，画期的な成果だという。
研究グループは今後，富岳などのスーパーコンピューターを活用し，電子状態計算が取り扱いに難渋する強相関系物質へのこの手法の適用を進めていくとしている。
