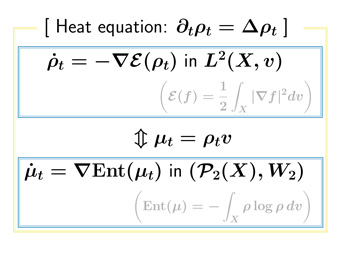東京工業大学，Nice大学，京都大学は共同研究により，必ずしも通常の可微分構造を持たない特異空間であるAlexandrov空間上で，2つの異なる方法で定義される熱分布が同一のものであることを証明した（ニュースリリース）。
更に，この結果を基に，空間の方位平均的な曲がり具合を記述するRicci曲率の理論の特異空間上での2つの定式化 –最適輸送理論による定式化と，Dirichletエネルギー汎関数の勾配曲線としての熱分布を用いた定式化– の間の関係を解明した。
熱分布の概念は，エネルギー汎関数の勾配曲線としての古典的解釈とは別に，最適輸送理論の枠組みでBoltzmannエントロピー汎関数の勾配曲線として定式化できる。この2つの定式化は特異空間上でも意味を持つが，それらの空間で同一の量を定めるかどうかは未解決であった。また，熱分布を用いたRicci曲率の理論は抽象的な枠組みで機能し，幅広い応用を持つ反面，理論適用の為の条件は可微分空間でしか検証されていなかった。
研究グループは今回，エントロピー汎関数の勾配曲線としての熱分布の，初期条件に対する解の一意性に問題を帰着させる全く新しい手法により，熱分布の2つの定式化を同定した。最適輸送理論に基づくRicci曲率の条件がエントロピー汎関数の凸性の度合いで表されることを同定結果と結合して，最適輸送理論と熱分布の理論の各々におけるRicci曲率の理論を結合した。
この研究成果を通じて，Ricci曲率の理論を熱分布の理論と組み合わせて理解する方法が特異空間において確立された。この観点は，より一般の特異空間へと理論を拡張し，それらの空間上で更なる幾何解析を展開する上での礎となっている。
